Question

如图，已知双曲线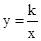，经过点D（6，1），点C是双曲线第三象限上的动点，过C作CA⊥x轴，过D作DB⊥y轴，垂足分别为A，B，连接AB，BC．

（1）求k的值；

（2）若△BCD的面积为12，求直线CD的解析式；

（3）判断AB与CD的位置关系，并说明理由．

 

Answer 1

【答案】

（1）6（2）（3）AB∥CD。理由见解析

【解析】解：（1）∵双曲线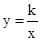经过点D（6，1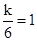），∴，解得k=6。

（2）设点C到BD的距离为h，

∵点D的坐标为（6，1），DB⊥y轴，∴BD=6，∴S_△BCD=×6•h=12，解得h=4。

∵点C是双曲线第三象限上的动点，点D的纵坐标为1，∴点C的纵坐标为1－4= －3。

∴，解得x= －2。∴点C的坐标为（－2，－3）。

设直线CD的解析式为y=kx＋b，

则，解得。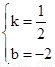

∴直线CD的解析式为。

（3）AB∥CD。理由如下：

∵CA⊥x轴，DB⊥y轴，点C的坐标为（－2，－3），点D的坐标为（6，1），

∴点A、B的坐标分别为A（－2，0），B（0，1）。

设直线AB的解析式为y=mx+n，

则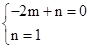，解得。

∴直线AB的解析式为。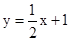

∵AB、CD的解析式k都等于相等。

∴AB与CD的位置关系是AB∥CD。

（1）把点D的坐标代入双曲线解析式，进行计算即可得解。

（2）先根据点D的坐标求出BD的长度，再根据三角形的面积公式求出点C到BD的距离，然后求出点C的纵坐标，再代入反比例函数解析式求出点C的坐标，然后利用待定系数法求一次函数解析式解答。

（3）根据题意求出点A、B的坐标，然后利用待定系数法求出直线AB的解析式，可知与直线

CD的解析式k值相等，所以AB、CD平行。