题目内容
如图所示，AB是⊙O的直径，AB=4，AC是弦，AC=
，则∠AOC为
| A．120° | B．1300 | C．140° | D．150° |
A
解析试题分析：作OD⊥AC，垂足为D，根据已知可求得OA，AD的长，再根据三角函数求得∠DOA的度数，从而可得到∠AOC的度数．
作OD⊥AC，垂足为D
∵AC=
∴AD=
∵AB=4
∴OA=2
∵sin∠DOA=
∴∠DOA=60°
∴∠AOC=120°．
故选A．
考点：垂径定理，正弦的概念
点评：解题的关键是读懂题意及图形，正确作出辅助线，构造直角三角形求解.
练习册系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
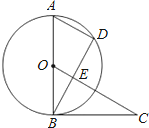如图所示，AB是⊙O的直径，AD是弦，∠DBC=∠A．
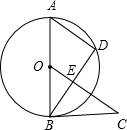如图所示，AB是⊙O的直径，AD是弦，∠DBC=∠A，OC⊥BD于点E．
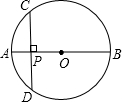如图所示，AB是⊙O的直径，弦CD⊥AB于点P，CD=10cm，AP：PB=1：5，则⊙O的半径为
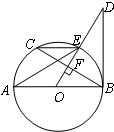如图所示，AB是⊙O直径，OD⊥弦BC于点F，且交⊙O于点E，且∠AEC=∠ODB．
如图所示，AB是⊙O直径，∠D=35°，则∠BOC等于（ ）