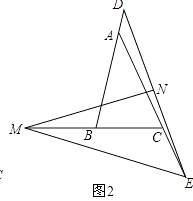
��Ŀ����
����Ŀ����ֱ֪��m��n����C��ֱ��m��һ�㣬��D��ֱ��n��һ�㣬CD��ֱ��m��n����ֱ����PΪ�߶�CD���е㣮
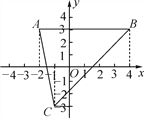
��1���������֣�ֱ��l��m��l��n������ֱ�ΪA��B������A���C�غ�ʱ����ͼ����ʾ��������PB����ֱ��д���߶�PA��PB��������ϵ���� ����
��2������֤������ͼ�ٵ�����£���ֱ��l����ƽ�Ƶ���ͼ�ڵ�λ�ã����ʣ�1���е�PA��PB�Ĺ�ϵʽ�Ƿ���Ȼ����������������֤����������������˵�����ɣ�
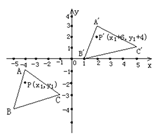
��3������̽������ͼ�ڵ�����£���ֱ��l�Ƶ�A��ת��ʹ�á�APB=90�㣨��ͼ����ʾ��������ƽ����m��n֮��ľ���Ϊ2k����֤��PAPB=kAB��

���𰸡�PA=PB��������PA=PB��
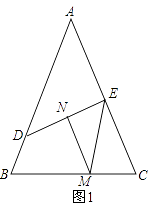
�������������������1������������CBD��ֱ�������Σ����ҵ�PΪ�߶�CD���е㣬Ӧ��ֱ�������ε����ʣ��ɵ�PA=PB���ݴ˽�ɣ���2�����ȹ�C��CE��n�ڵ�E������PE��Ȼ��ֱ��жϳ�PC=PE����PCA=��PEB��AC=BE��Ȼ�����ȫ���������ж��ķ������жϳ���PAC�ס�PBE�������жϳ�PA=PB��Ȼ��������3�������ӳ�AP��ֱ��n�ڵ�F����AE��BD�ڵ�E��Ȼ����������������ж��ķ������жϳ���AEF�ס�BPF�������жϳ�AFBP=AEBF���ٸ�AF=2PA��AE=2k��BF=AB���ɵ�2PAPB=2k��AB������PAPB=kAB���ݴ˽��
�����������1����l��n�� ��BC��BD�� ��������CBD��ֱ�������Σ� ������PΪ�߶�CD���е㣬
��PA=PB��
��ֱ��l����ƽ�Ƶ���ͼ����λ�ã�PA=PB��Ȼ�������������£�
��ͼ������C��CE��n�ڵ�E������PE��
 ��
��
��������CED��ֱ�������Σ���PΪ�߶�CD���е㣬 ��PD=PE�� ������PΪ�߶�CD���е㣬
��PC=PD�� ��PC=PE�� ��PD=PE�� ���CDE=��PEB�� ��ֱ��m��n�� ���CDE=��PCA��
���PCA=��PEB�� ����ֱ��l��m��l��n��CE��m��CE��n�� ��l��CE�� ��AC=BE��
����PAC����PBE�У� ���PAC�ס�PBE�� ��PA=PB��
���PAC�ס�PBE�� ��PA=PB��
��3����ͼ�����ӳ�AP��ֱ��n�ڵ�F����AE��BD�ڵ�E��
 ��
��
��ֱ��m��n�� ��![]() �� ��AP=PF�� �ߡ�APB=90���� ��BP��AF�� ����AP=PF�� ��BF=AB��
�� ��AP=PF�� �ߡ�APB=90���� ��BP��AF�� ����AP=PF�� ��BF=AB��
����AEF����BPF�У�![]() ���AEF�ס�BPF�� ��
���AEF�ס�BPF�� ��![]() �� ��AFBP=AEBF��
�� ��AFBP=AEBF��
��AF=2PA��AE=2k��BF=AB�� ��2PAPB=2k��AB�� ��PAPB=kAB�� ��PA=PB

 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�����Ŀ��Ϊ�˸�������ij��ˮ�ʣ����������������۹�˾��������![]() ̨��ˮ�����豸������
̨��ˮ�����豸������![]() ��
��![]() �����ͺŵ��豸������ÿ̨�ļ۸��´�����ˮ�����±��������飺����һ̨
�����ͺŵ��豸������ÿ̨�ļ۸��´�����ˮ�����±��������飺����һ̨![]() ���豸�ȹ���һ̨
���豸�ȹ���һ̨![]() ���豸��
���豸��![]() ��Ԫ������
��Ԫ������![]() ̨
̨![]() ���豸�ȹ���
���豸�ȹ���![]() ̨
̨![]() ���豸��
���豸��![]() ��Ԫ��
��Ԫ��
|
| |
�۸���Ԫ/̨�� |
|
|
������ˮ������/�£� |
|
|
��![]() ����
����![]() ��
��![]() ��ֵ��
��ֵ��
��![]() ����Ԥ�㣺�����۹�˾������ˮ�����豸���ʽ���
����Ԥ�㣺�����۹�˾������ˮ�����豸���ʽ���![]() ��Ԫ������Ϊ�ù�˾���ļ��ֹ�����
��Ԫ������Ϊ�ù�˾���ļ��ֹ�����
��![]() ���ڣ�
���ڣ�![]() ���ʵ������£���ÿ��Ҫ�����ú�����ˮ��������
���ʵ������£���ÿ��Ҫ�����ú�����ˮ��������![]() �֣�Ϊ�˽�Լ�ʽ�����Ϊ���۹�˾���һ����ʡǮ�Ĺ�����
�֣�Ϊ�˽�Լ�ʽ�����Ϊ���۹�˾���һ����ʡǮ�Ĺ�����