题目内容
⊙O的半径为1cm,弦AB= cm,AC=
cm,AC= cm,则∠BAC的度数为 .
cm,则∠BAC的度数为 .
【答案】分析:分两种情况考虑:当圆心O在弦AC与AB之间时,如图(1)所示,过O作OD⊥AB,OE⊥AC,连接OA,由垂径定理得到:D为AB中点,E为AC中点,求出AE与AD的长,在直角三角形AEO与ADO中,利用锐角三角函数定义及特殊角的三角函数值求出∠CAO与∠BAO的度数,即可求出∠BAC的度数;当圆心在弦AC与AB一侧时,如图(2)所示,同理∠BAC的度数.
解答: 解:当圆心O在弦AC与AB之间时,如图(1)所示,
解:当圆心O在弦AC与AB之间时,如图(1)所示,
过O作OD⊥AB,OE⊥AC,连接OA,
由垂径定理得到:D为AB中点,E为AC中点,
∴AE= AC=
AC= cm,AD=
cm,AD= AB=
AB= cm,
cm,
∴cos∠CAO= =
= ,cos∠BAO=
,cos∠BAO= =
= ,
,
∴∠CAO=30°,∠BAO=45°,
此时∠BAC=30°+45°=75°;
当圆心在弦AC与AB一侧时,如图(2)所示,同理得:∠BAC=45°-30°=15°,
综上,∠BAC=15°或75°.
故答案为:15°或75°.
点评:此题考查了垂径定理,锐角三角函数定义,特殊角的三角函数值,利用了分类讨论的思想,熟练掌握垂径定理是解本题的关键.
解答:
 解:当圆心O在弦AC与AB之间时,如图(1)所示,
解:当圆心O在弦AC与AB之间时,如图(1)所示,过O作OD⊥AB,OE⊥AC,连接OA,
由垂径定理得到:D为AB中点,E为AC中点,
∴AE=
 AC=
AC= cm,AD=
cm,AD= AB=
AB= cm,
cm,∴cos∠CAO=
 =
= ,cos∠BAO=
,cos∠BAO= =
= ,
,∴∠CAO=30°,∠BAO=45°,
此时∠BAC=30°+45°=75°;
当圆心在弦AC与AB一侧时,如图(2)所示,同理得:∠BAC=45°-30°=15°,
综上,∠BAC=15°或75°.
故答案为:15°或75°.
点评:此题考查了垂径定理,锐角三角函数定义,特殊角的三角函数值,利用了分类讨论的思想,熟练掌握垂径定理是解本题的关键.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 10、如图,⊙O的圆心O到直线l的距离为3cm,⊙O的半径为1cm,将直线l向右(垂直于l的方向)平移,使l与⊙O相切,则平移的距离为( )
10、如图,⊙O的圆心O到直线l的距离为3cm,⊙O的半径为1cm,将直线l向右(垂直于l的方向)平移,使l与⊙O相切,则平移的距离为( )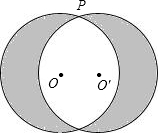 如图,点P是⊙O上一点,⊙O的半径为1cm,以点P为旋转中心,把⊙O逆时针旋转60°得到⊙O′,则图中阴影部分面积是
如图,点P是⊙O上一点,⊙O的半径为1cm,以点P为旋转中心,把⊙O逆时针旋转60°得到⊙O′,则图中阴影部分面积是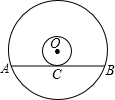 如图是一张电脑光盘的表面,两个圆的圆心都是点O,大圆的弦AB所在直线是小圆的切线,切点为C.已知大圆的半径为5cm,小圆的半径为1cm,则弦AB的长度为
如图是一张电脑光盘的表面,两个圆的圆心都是点O,大圆的弦AB所在直线是小圆的切线,切点为C.已知大圆的半径为5cm,小圆的半径为1cm,则弦AB的长度为