题目内容
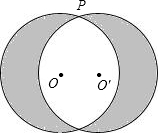 如图,点P是⊙O上一点,⊙O的半径为1cm,以点P为旋转中心,把⊙O逆时针旋转60°得到⊙O′,则图中阴影部分面积是
如图,点P是⊙O上一点,⊙O的半径为1cm,以点P为旋转中心,把⊙O逆时针旋转60°得到⊙O′,则图中阴影部分面积是分析:根据题意,连接两圆心与两圆的交点的半径,知阴影部分的面积等于两圆的面积减去两扇形的面积+菱形的面积,从而根据扇形的面积公式,易算出阴影部分的面积.
解答: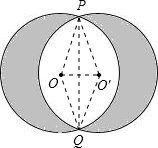 解:连接OP,O′P,则∠OPO′=60°,∠QOP=120°
解:连接OP,O′P,则∠OPO′=60°,∠QOP=120°
扇形QOP的面积=
=
=
(cm2)
同理扇形QO′P的面积=
=
=
(cm2)
而菱形OQO′P的面积=
OO′•PQ=
•1•2•
=
(cm2)
故阴影部分的面积是:2×(2π-
+
)=
+
(cm2)
 解:连接OP,O′P,则∠OPO′=60°,∠QOP=120°
解:连接OP,O′P,则∠OPO′=60°,∠QOP=120°扇形QOP的面积=
| nπr2 |
| 360 |
| 120π12 |
| 360 |
| π |
| 3 |
同理扇形QO′P的面积=
| nπr2 |
| 360 |
| 120π12 |
| 360 |
| π |
| 3 |
而菱形OQO′P的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
故阴影部分的面积是:2×(2π-
| 2π |
| 3 |
| ||
| 2 |
| 2π |
| 3 |
| 3 |
点评:本题考查旋转的性质,扇形的面积公式等.旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.

练习册系列答案
相关题目
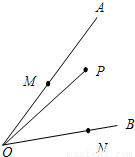
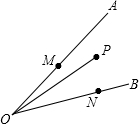 如图:点P是∠AOB内一定点,点M、N分别在边OA、OB上运动,若∠AOB=30°,OP=3
如图:点P是∠AOB内一定点,点M、N分别在边OA、OB上运动,若∠AOB=30°,OP=3 如图:点P是∠AOB内一定点,点M、N分别在边OA、OB上运动,若∠AOB=45°,OP=
如图:点P是∠AOB内一定点,点M、N分别在边OA、OB上运动,若∠AOB=45°,OP= 如图,点O是AB上的一点,OC为任意一条射线,另有OD,OE分别平分∠AOC,∠BOC.
如图,点O是AB上的一点,OC为任意一条射线,另有OD,OE分别平分∠AOC,∠BOC.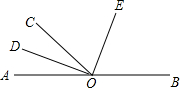 如图,点O是AB上的一点,OC为任意一条射线,另有OD,OE分别平分∠AOC,∠BOC.
如图,点O是AB上的一点,OC为任意一条射线,另有OD,OE分别平分∠AOC,∠BOC. ,则△PMN的周长的最小值为 .
,则△PMN的周长的最小值为 .