Question

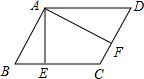如图，?ABCD的周长为54，AE⊥BC，AF⊥CD，且AE=4，AF=5，且∠EAF=58°，则∠BAD=________°，?ABCD面积为________．

Answer 1

122    60
分析：由垂直的性质和四边形的内角和为360°可求出∠BAD的度数；已知平行四边形的高AE、AF，设BC=xcm，则CD=（27-x）cm，根据“等面积法”列方程，求BC，从而求出平行四边形的面积．
解答：∵AE⊥BC，AF⊥CD，
∴∠AEC=∠AFC=90°，
∴∠C=∠BAD=360°-90°-90°-58°=122°，
故答案为：122；
设BC=xcm，则CD=（27-x）cm，根据“等面积法”得
4x=5（27-x），解得x=15，
∴平行四边形ABCD的面积=4x=4×15=60，
故答案为：60
点评：本题考查了平行四边形的性质，应用的知识点为：平行四边形一组邻边之和为平行四边形周长的一半，平行四边形的面积=底×高，可用两种方法表示．