题目内容
已知：点A（x1，y1）、B（x2，y2）、C（x3，y3）是函数y=-
图象上的三点，且x1＜0＜x2＜x3则y1、y2、y3的大小关系是（ ）
| 3 |
| x |
| A、y1＜y2＜y3 |
| B、y2＜y3＜y1 |
| C、y3＜y2＜y1 |
| D、无法确定 |
分析：对y=-
，由x1＜0＜x2＜x3知，A点位于第二象限，y1最大，第四象限，y随x增大而增大，y2＜y3，故y2＜y3＜y1．
| 3 |
| x |
解答：解：∵y=-
中k=-3＜0，
∴此函数的图象在二、四象限，
∵点A（x1，y1）、B（x2，y2）、C（x3，y3）是函数y=-
图象上的三点，且x1＜0＜x2＜x3，
∴A点位于第二象限，y1＞0，B、C两点位于第四象限，
∵0＜x2＜x3，
∴y2＜y3，
∴y2＜y3＜y1．
故选B．
| 3 |
| x |
∴此函数的图象在二、四象限，
∵点A（x1，y1）、B（x2，y2）、C（x3，y3）是函数y=-
| 3 |
| x |
∴A点位于第二象限，y1＞0，B、C两点位于第四象限，
∵0＜x2＜x3，
∴y2＜y3，
∴y2＜y3＜y1．
故选B．
点评：本题考查了反比例函数图象上点的坐标特征，要学会比较图象上点的坐标．
练习册系列答案
相关题目
已知三点P1（x1，y1），P2（x2，y2），P3（1，-2）都在反比例函数y=
的图象上，若x1＜0，x2＞0，则下列式子正确的是（ ）
| k |
| x |
| A、y1＜y2＜0 |
| B、y1＜0＜y2 |
| C、y1＞y2＞0 |
| D、y1＞0＞y2 |
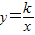的图象上，若x1＜0，x2＞0，则下列式子正确的是（ ）