题目内容
(2009•河西区一模)如图是一块梯形铁片的残余部分,量出∠A=120°,∠B=105°,AB=20cm,并且还知道原来梯 形铁片的另一底边比AB长10cm.
形铁片的另一底边比AB长10cm.
(1)求原来梯形铁片的∠D和∠C的度数.
(2)求原来梯形铁片的另外三条边的长度.
 形铁片的另一底边比AB长10cm.
形铁片的另一底边比AB长10cm.(1)求原来梯形铁片的∠D和∠C的度数.
(2)求原来梯形铁片的另外三条边的长度.
分析:(1)由梯形的性质可知:∠A+∠D=180°,∠B+∠C=180°,继而可求出答案;
(2)过点B作BE∥DA交DC与E,作CF⊥BE于F,先求出DC的长,然后在Rt△CEF和Rt△CBF中,分别解直角三角形即可求出AD和BC的长.
(2)过点B作BE∥DA交DC与E,作CF⊥BE于F,先求出DC的长,然后在Rt△CEF和Rt△CBF中,分别解直角三角形即可求出AD和BC的长.
解答:解:(1)由题意得:∠A+∠D=180°,∠B+∠C=180°,
∵∠A=120°,∠B=105°,
∴∠D=60°,∠C=75°;
(2)过点B作BE∥DA交DC于E,作CF⊥BE于F,
 ∴四边形DABE是平行四边形,
∴四边形DABE是平行四边形,
∴∠D=∠BEC=∠ABE=60°,DE=AB=20,
∴CE=10,DC=30,
在Rt△CEF中,可知∠ECF=30°,
∴EF=
CE=5,CF=10×sin60°=5
,
在Rt△CBF中,△FCB=△FBC=∠ABC-∠ABE=105°-60°=45°,
∴CB=
=5
•
=5
,BF=CF=5
,
∴AD=BE=EF+BF=5+5
.
∵∠A=120°,∠B=105°,
∴∠D=60°,∠C=75°;
(2)过点B作BE∥DA交DC于E,作CF⊥BE于F,
 ∴四边形DABE是平行四边形,
∴四边形DABE是平行四边形,∴∠D=∠BEC=∠ABE=60°,DE=AB=20,
∴CE=10,DC=30,
在Rt△CEF中,可知∠ECF=30°,
∴EF=
| 1 |
| 2 |
| 3 |
在Rt△CBF中,△FCB=△FBC=∠ABC-∠ABE=105°-60°=45°,
∴CB=
| CF |
| sin45° |
| 3 |
| 2 |
| 6 |
| 3 |
∴AD=BE=EF+BF=5+5
| 3 |
点评:本题考查梯形的知识,同时设计了直角三角形和平行四边形的性质,有一定难度,解题关键是正确作出辅助线.

练习册系列答案
相关题目
 (2009•河西区一模)如图所示,在半径为r的圆内作一个内接正三角形,依次再作内切圆,那么图中最小的圆的半径是( )
(2009•河西区一模)如图所示,在半径为r的圆内作一个内接正三角形,依次再作内切圆,那么图中最小的圆的半径是( ) (2009•河西区一模)如图,已知PA,PB分别切⊙O于A、B,CD切⊙O于E,PO=13,AO=5,则△PCD周长为
(2009•河西区一模)如图,已知PA,PB分别切⊙O于A、B,CD切⊙O于E,PO=13,AO=5,则△PCD周长为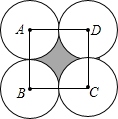 (2009•河西区一模)如图,正方形的边长为a,分别以正方形的四个顶点为圆心,以
(2009•河西区一模)如图,正方形的边长为a,分别以正方形的四个顶点为圆心,以 点P,连接AB和ED.
点P,连接AB和ED.