Question

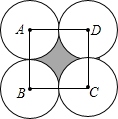（2009•河西区一模）如图，正方形的边长为a，分别以正方形的四个顶点为圆心，以

a

2

为半径作圆，则图中的阴影面积为

4-π

4

a²

．

Answer 1

分析：求得正方形ABCD的面积，和四个扇形的面积的和然后相减即可求解．

解答：解：正方形ABCD的面积是：a²；
四个扇形的面积是：π×(

a

2

)2=

a2

4

π．
则阴影部分的面积是：a2-

πa2

4

=

4-π

4

a²．
故答案是：

4-π

4

a²．

点评：本题主要考查了扇形的面积的计算，正确求得四个扇形的面积的和是解题的关键．