题目内容
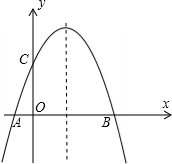
 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,图象过A点(3,0),对称轴为,给出三个结论:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-1和3;④8a+c<0.其中正确的命题是________.
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,图象过A点(3,0),对称轴为,给出三个结论:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-1和3;④8a+c<0.其中正确的命题是________.
②③④
分析:先会观察图形,知a<0,c>0,由- =1,b2-4ac>0,可判断出②③④小题的正确与否,①小题知当x=1时y的值,利用图象就可求出答案.
=1,b2-4ac>0,可判断出②③④小题的正确与否,①小题知当x=1时y的值,利用图象就可求出答案.
解答:由图象知;当x=1时y=ax2+bx+c=a×12+b×1+c=a+b+c>0,
∴①不正确;
∵- =1>0,
=1>0,
∴b>2a,
∴②正确;
∵图象过A点(3,0),对称轴为x=1,
∴ax2+bx+c=0的两根分别为-1和3,
∴③正确;
∵图象过A点(3,0),
∴0=9a+3b+c,
∵- =1,
=1,
∴b=-2a,
∴8a+c<0,
∴④正确;
故答案为②③④.
点评:解此题的关键是数形有机结合,能根据图象看出a b c 的符号,与X轴,Y轴交点能确定cb2-4ac的正负,(两个交点b2-4ac>0,一个交点b2-4ac=0,无交点时b2-4ac<0),进而求出答案.
分析:先会观察图形,知a<0,c>0,由-
 =1,b2-4ac>0,可判断出②③④小题的正确与否,①小题知当x=1时y的值,利用图象就可求出答案.
=1,b2-4ac>0,可判断出②③④小题的正确与否,①小题知当x=1时y的值,利用图象就可求出答案.解答:由图象知;当x=1时y=ax2+bx+c=a×12+b×1+c=a+b+c>0,
∴①不正确;
∵-
 =1>0,
=1>0,∴b>2a,
∴②正确;
∵图象过A点(3,0),对称轴为x=1,
∴ax2+bx+c=0的两根分别为-1和3,
∴③正确;
∵图象过A点(3,0),
∴0=9a+3b+c,
∵-
 =1,
=1,∴b=-2a,
∴8a+c<0,
∴④正确;
故答案为②③④.
点评:解此题的关键是数形有机结合,能根据图象看出a b c 的符号,与X轴,Y轴交点能确定cb2-4ac的正负,(两个交点b2-4ac>0,一个交点b2-4ac=0,无交点时b2-4ac<0),进而求出答案.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 如图,是二次函数y=ax2+bx+c的图象,则下列说法错误的是( )
如图,是二次函数y=ax2+bx+c的图象,则下列说法错误的是( )| A、a<0 | ||
B、对称轴是直线x=-
| ||
| C、ab<0 | ||
D、x>-
|
 6、如图,是二次函数y=ax2+bx+c的图象,点P(a+b,ac)是平面直角坐标系内的点,则点P在( )
6、如图,是二次函数y=ax2+bx+c的图象,点P(a+b,ac)是平面直角坐标系内的点,则点P在( ) 下列说法正确的是
下列说法正确的是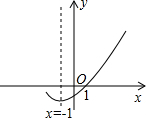 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分, 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,则方程ax2+bx+c=0的两根分别为
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,则方程ax2+bx+c=0的两根分别为