题目内容
如图，⊙O中， | AE |
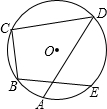
分析：由图可知：
、
、
正好构成整个圆，即它们的度数和为360°，由此可得
+
=320°，那么两段弧所对的圆心角的度数和也为320°，根据圆周角定理即可求得∠B+∠D的值．
|
| CDE |
|
| CBA |
|
| AE |
|
| CDE |
|
| CBA |
解答：解：∵
=40°，
∴
+
=360°-40°=320°；
∴∠B+∠D=160°．
|
| AE |
∴
|
| CDE |
|
| CBA |
∴∠B+∠D=160°．
点评：此题综合考查了圆心角、弧的关系，及圆周角定理的应用；能够正确的求得∠B、∠D所对弧的度数是解答此题的关键．
练习册系列答案
相关题目
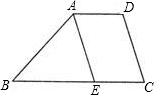
29、如图，?ABCD中，AE⊥CD于E，∠B=55°，则∠DAE等于（ ）
（2013•沈阳）如图，△ABC中，AE交BC于点D，∠C=∠E，AD=4，BC=8，BD：DC=5：3，则DE的长等于（ ）
如图，△ABC中，AE是∠BAC的角平分线，AD是BC边上的高线，且∠B=50°，∠C=60°，则∠EAD的度数是
如图，△ABC中，AE⊥BC于E，AD是△ABC的角平分线，若∠ACB=40°，∠BAE=30°，则∠EAD=