题目内容
已知a,b分别满足a2+2b=21-ab和b2+2a=27-ab,求a+b的值.
考点:因式分解的应用
专题:
分析:把等式a2+2b=21-ab和b2+2a=27-ab两边分别相加,进一步整理利用完全平方公式分解因式求得答案即可.
解答:解:∵a2+2b=21-ab,b2+2a=27-ab,
∴a2+2b+b2+2a=21-ab+27-ab,
∴a2+2ab+b2+2a+2b=48,
∴(a+b)2+2(a+b)+1=49,
∴(a+b+1)2=49,
∴a+b+1=±7,
∴a+b=6或a+b=-8.
∴a2+2b+b2+2a=21-ab+27-ab,
∴a2+2ab+b2+2a+2b=48,
∴(a+b)2+2(a+b)+1=49,
∴(a+b+1)2=49,
∴a+b+1=±7,
∴a+b=6或a+b=-8.
点评:此题考查因式分解的实际运用,掌握完全平方公式是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个几何体的主视图和左视图都是矩形,俯视图是一个圆,那么这个几何体可能是( )
| A、直棱柱 | B、圆柱 | C、圆锥 | D、球 |
下列所描述的事件是必然事件的是( )
| A、打开电视机,正在转播足球赛 |
| B、射击运动员射击一次,命中10环 |
| C、通常水加热到100℃时沸腾 |
| D、在一个只装有红球袋中摸出白球 |
如果
=
,那么
的值为( )
| x+y |
| 3x |
| 1 |
| 2 |
| y |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
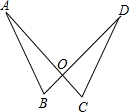 如图,线段AC、DB的交于点O,且AC=BD,OB=OC,小明在探索△ABO与△DCO全等时,他的思考过程如下:因为AC=DB,∠AOB=∠DOC,OB=OC,所以△ABD≌△DCO.
如图,线段AC、DB的交于点O,且AC=BD,OB=OC,小明在探索△ABO与△DCO全等时,他的思考过程如下:因为AC=DB,∠AOB=∠DOC,OB=OC,所以△ABD≌△DCO. 已知四边形ABCD中,AB∥CD,∠1=∠2,∠3=∠4,求证:BC=AB+CD.
已知四边形ABCD中,AB∥CD,∠1=∠2,∠3=∠4,求证:BC=AB+CD.