题目内容
13. 矩形两条对角线的夹角为∠AOB=60°,则∠ACB的度数为( )
矩形两条对角线的夹角为∠AOB=60°,则∠ACB的度数为( )| A. | 60° | B. | 15° | C. | 30° | D. | 45° |
分析 根据矩形的性质和三角形内角与外角的关系,求解即可.
解答 解:∵矩形ABCD中,对角线AC与BD相交于O点,
∴OB=OC,∠OBC=∠OCB,
∵∠AOB是△OBC的外角,
∴∠AOB=∠OBC+∠ACB=60°,
∴∠ACB=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×60°=30°.
故选C.
点评 本题考查的是矩形的性质及三角形内角与外角的关系.熟记矩形的各种性质以及三角形内角和定理及其外角和定理是解题关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
3.如果3x=m,3y=n,那么3x-y等于( )
| A. | m+n | B. | m-n | C. | mn | D. | $\frac{m}{n}$ |
5.已知二次函数y=2(x+a)2+b的顶点坐标为(2,-3),则a,b的值分别为( )
| A. | 2,-3 | B. | -2,-3 | C. | 2,3 | D. | -2,3 |
3. 如图,若∠AOB=∠COD,那么( )
如图,若∠AOB=∠COD,那么( )
 如图,若∠AOB=∠COD,那么( )
如图,若∠AOB=∠COD,那么( )| A. | ∠1>∠2 | B. | ∠1<∠2 | ||
| C. | ∠1=∠2 | D. | ∠1、∠2的大小不确定 |
 如图,圆O的半径为6,点A、B、C在圆O上,且∠ACB=45°,则点O到弦AB的距离为3$\sqrt{2}$.
如图,圆O的半径为6,点A、B、C在圆O上,且∠ACB=45°,则点O到弦AB的距离为3$\sqrt{2}$.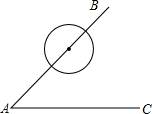 如图所示,∠BAC=60°,O是射线AB上一点,以O为圆心,$\frac{1}{2}$OA的长为半径的⊙O,将AC绕点A逆时针旋转30°时,AC与⊙O相切.
如图所示,∠BAC=60°,O是射线AB上一点,以O为圆心,$\frac{1}{2}$OA的长为半径的⊙O,将AC绕点A逆时针旋转30°时,AC与⊙O相切.