题目内容
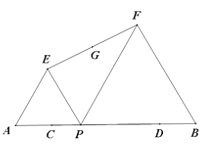
【题目】如图,在四边形ABCD中,AD//BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.
(1)DAE 和CFE全等吗?说明理由;
(2)若AB BCAD,说明 BE AF;
(3)在(2)的条件下,若CE 5,D 90 ,求出E到AB的距离.
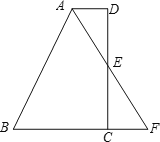
【答案】(1)全等,理由见解析;(2)详见解析;(3)点E到AB的距离为5.
【解析】
(1)根据ASA证三角形全等即可;(2)根据等腰三角形三线合一的性质即可说明;(3)根据角平分线的性质可得E到AB的距离.
解:(1)![]()
![]()
∵E 是 DC 的中点
![]() DE CE
DE CE
在ADE和FCE中
![]() ,
,![]()
DAE CFE
(2)由DAE CFE可得AD CF
AB BCADBCCF BF
连接BE,在等腰ABF中,E为CD的中点
BE AF

(3)过点 E 作 EG AB 于点G
由(1)(2)可知![]() 平分
平分![]()
![]()
∵EBC EBG, BE BE, BGE BCE
GBE CBE
∴GE=EC=5,
∴点E到AB的距离为5.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
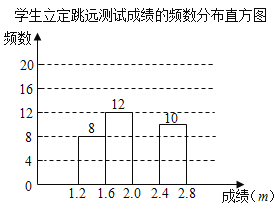
【题目】为了解某校八年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:![]() )绘制成不完整的频数分布表和频数分布直方图.
)绘制成不完整的频数分布表和频数分布直方图.
学生立定路远测试成绩的频数分布表
分组 | 频数 |
|
|
| 12 |
|
|
| 10 |
请根据图表中所提供的信息,完成下列问题:
(1)求表中![]() ,
,![]() 的值;
的值;
(2)请把频数分布直方图补充完整;
(3)该校八年级共有800名学生,估计该年级学生立定跳远成绩在![]() 范围内的学生有多少人?
范围内的学生有多少人?