题目内容
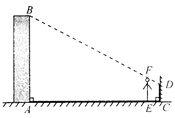
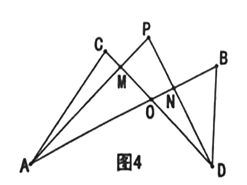
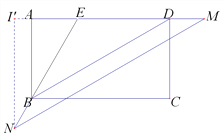
【题目】在矩形ABCD中,BC=6,点E是AD边上一点,∠ABE=30°,BE=DE,连接BD.动点M从点E出发沿射线ED运动,过点M作MN∥BD交直线BE于点N.
(1)如图1,当点M在线段ED上时,求证:MN=![]() EM;
EM;
(2)设MN长为x,以M、N、D为顶点的三角形面积为y,求y关于x的函数关系式;
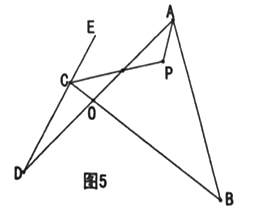
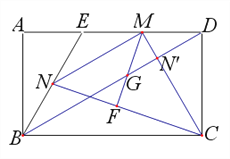
(3)当点M运动到线段ED的中点时,连接NC,过点M作MF⊥NC于F,MF交对角线BD于点G(如图2),求线段MG的长.

【答案】(1)证明见解析(2)![]() (3)
(3)![]()
【解析】分析:(1)先根据等角对等边证明EM=EN, 过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() .
.
在Rt△EMH中,根据锐角三角函数求出MH与EM的数量关系,进而可证明结论;
(2)点M从点E出发沿射线ED运动,所以分当点M在线段ED上时与当点M在线段ED的延长线上时两种情况讨论,根据所作的辅助线,可得y与x的关系;
(3)连接CM交BD于点![]() ,可得∠NMC=90°,进而可得
,可得∠NMC=90°,进而可得![]() ∽
∽![]() ,可得
,可得![]() ,解之可得MG的长.
,解之可得MG的长.
详解:(1)证明:∵![]() °,
°, ![]() ° ,
° ,
∴ ![]() °
°
∵![]() ,
,
∴![]()
![]() °
°
∵![]() ∥
∥![]() ,
,
∴![]()
∴![]() °,
°,
∴![]()
过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() .
.
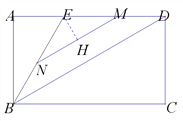
在![]() 中,
中,![]()
∴![]()
∴![]()
(2)在![]() 中,
中,![]() ,
,![]()
∴![]()
∵![]() ∴
∴![]()
a.当点![]() 在线段
在线段![]() 上时,过点
上时,过点![]() 作
作![]() 于点
于点![]() ,
,
在![]() 中,
中,![]()
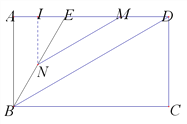
由(1)可知:
![]() ,
,
∴![]()
∴![]()
∴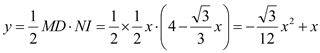
b.当点![]() 在线段
在线段![]() 延长线上时,过点
延长线上时,过点![]() 作
作![]() 于点
于点![]()
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴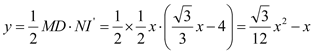 ;
;
(3)连接![]() ,交
,交![]() 于点
于点![]() .
.
∵![]() 为
为![]() 的中点 ,
的中点 ,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ∥
∥![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() .
.
点睛:本题结合矩形的性质,平行线的判定与性质,等腰三角形的判定与性质,二次函数的综合应用,解直角三角形,相似三角形的判定与性质,解答本题的关键是熟练掌握各种图形的判定与性质,.

【题目】有这样一个问题:探究函数![]() 的图象与性质.小东根据学习函数的经验,对函数
的图象与性质.小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … | -3 | -2 | -1 |
| 1 | 2 | 3 | 4 | 5 | … |
y | … |
|
|
|
| 3 |
|
|
| m | … |
求m的值;
(3)如下图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)结合函数的图象,写出该函数的一条性质: .