题目内容
我们已经知道字母可以表示任意有理数或无理数．已知(2x-1)3=a3x3+a2x2+a1x+a0，则a0+a2的值为（ ）
| A、9 | B、-13 | C、-27 | D、7 |
考点：代数式求值
专题：计算题
分析：已知等式左边变形后，利用完全平方公式展开，再利用多项式乘以多项式法则计算得到结果，确定出a0与a2的值，即可求出a0+a2的值．
解答：解：（2x-1）3=（2x-1）（2x-1）2=（2x-1）（4x2-4x+1）=8x3-8x2+2x-4x2+4x-1=8x3-12x2+6x-1，
∴a0=-1，a2=-12，
则a0+a2=-1-12=-13．
故选B．
∴a0=-1，a2=-12，
则a0+a2=-1-12=-13．
故选B．
点评：此题考查了代数式求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
下列一组各数是无理数的是（ ）
A、0.
| ||
B、
| ||
C、
| ||
| D、2.626626662 |
酒桶空了30%时，所装的酒比它装了30%时多了30L．请问酒桶装满时能装多少升？（ ）
| A、60 | B、75 | C、90 | D、100 |
下列各多项式的乘法中，能利用平方差公式计算的是（ ）
| A、（1+x）（x+1） | ||||
| B、（-a+b）（a-b） | ||||
C、(
| ||||
| D、（x2-y）（y2+x） |
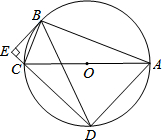如图，⊙O是Rt△ABC的外接圆，∠ABC=90°，AC=13，BC=5，弦BD=BA，BE⊥DC交DC的延长线于点E．