Question

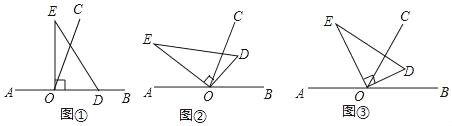
【题目】（原题）已知直线AB∥CD，点P为平行线AB，CD之间的一点．如图1，若∠ABP=50°，∠CDP=60°，BE平分∠ABP，DE平分∠CDP，求∠BED的度数．

（探究）如图2，当点P在直线AB的上方时，若∠ABP=α，∠CDP=β，∠ABP和∠CDP的平分线交于点E1，∠ABE1与∠CDE1的角平分线交于点E2，∠ABE2与∠CDE2的角平分线交于点E3，…以此类推，求∠En的度数．

（变式）如图3，∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E，试猜想∠P与∠E的数量关系，并说明理由．

Answer 1

【答案】【原题】55°；【探究】∠En的度数为（β﹣α）；【变式】∠DEB=90°﹣∠P．理由见解析.

【解析】

过E作EF∥AB，依据平行线的性质，即可得到∠BED=∠BEF+∠DEF=∠ABE+∠CDE，依据角平分线即可得出∠BED的度数；【探究】依据平行线的性质以及三角形外角性质，求得∠E1=（β﹣α），∠E2=（β﹣α），∠E3=（β﹣α），以此类推∠En的度数为（β﹣α）；【变式】过E作EG∥AB，进而得出∠DEB=∠BEG+∠DEG=∠MBE+∠FDE=∠ABQ+∠FDE，再根据平行线的性质以及三角形外角性质，即可得到∠DEB=90°﹣（∠CDP﹣∠ABP）=90°﹣（∠AHP﹣∠ABP）=90°﹣∠P．

如图1，过E作EF∥AB，而AB∥CD，

∴AB∥CD∥EF，

∴∠ABE=∠FEB，∠CDE=∠FED，

∴∠BED=∠BEF+∠DEF=∠ABE+∠CDE，

又∵∠ABP=50°，∠CDP=60°，BE平分∠ABP，DE平分∠CDP，

∴∠ABE=∠ABP=25°，∠CDE=∠CDP=30°，

∴∠BED=25°+30°=55°，

故答案为：55°；

【探究】

如图2，∵∠ABP和∠CDP的平分线交于点E1，

∴∠ABE1=∠ABP=α，∠CDE1=∠CDP=，

∵AB∥CD，

∴∠CDF=∠AFE1=，

∴∠E1=∠AFE1﹣∠ABE1=﹣α=（β﹣α），

∵∠ABE1与∠CDE1的角平分线交于点E2，

∴∠ABE2=∠ABE1=α，∠CDE2=∠CDE1=，

∵AB∥CD，

∴∠CDG=∠AGE2=，

∴∠E2=∠AGE2﹣∠ABE2=（β﹣α），

同理可得，∠E3=（β﹣α），

以此类推，∠En的度数为（β﹣α）．

【变式】

∠DEB=90°﹣∠P．理由如下：

如图3，过E作EG∥AB，而AB∥CD，

∴AB∥CD∥EG，

∴∠MBE=∠BEG，∠FDE=∠GED，

∴∠DEB=∠BEG+∠DEG=∠MBE+∠FDE=∠ABQ+∠FDE，

又∵∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E，

∴∠FDE=∠PDF=（180°﹣∠CDP），∠ABQ=∠ABP，

∴∠DEB=∠ABP+（180°﹣∠CDP）=90°﹣（∠CDP﹣∠ABP），

∵AB∥CD，

∴∠CDP=∠AHP，

∴∠DEB=90°﹣（∠CDP﹣∠ABP）=90°﹣（∠AHP﹣∠ABP）=90°﹣∠P．