题目内容
探究问题:圆内有很多关于线段的性质,如果能进行深入的探究,对提高自己的学习能力有很大的帮助。虽然这些知识看起来很复杂,摸不着头脑,但其实,我们完全可以用已经学习过的知识来得到这些新的知识。下面,就请同学们开动脑筋,积极思考,来作一个深入的探究吧。
如图所示,PT是圆O的切线,点T是切点,作线段PB与圆O相交,交点为A、B两点,连结TA、OP,OP与圆O相交于点C。
(1)探究∠ATP与∠B之间的关系(提示:过点T作直径与圆相交,连结这个交点与A点)
(2)证明:PT2=PA·PB
(3)如果线段PA=4,AB=5,CP=3,求出圆O的半径。
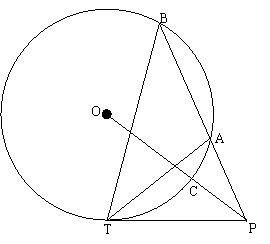 |
解:(1)连结OT并延长交圆O于点C,连结AC.
因为TC是直径,故∠TAC是直角,也就是∠ACT与∠CTA互余.
又因为∠TCA和∠B所对弧相同,所以∠TCA=∠B,故∠B与∠CTA互余. (4分)
又PT是切线,所以∠CTA和∠ATP互余,所以∠ATP=∠B.
(2)因为∠ATP=∠B,∠TP=∠BPA,所以ΔATP ΔTPB,于是
ΔTPB,于是
 ,所以PT2=PA·PB (7分)
,所以PT2=PA·PB (7分)
(3)因为PA=4,AB=5,所以PB=9,从而PT2=PA·PB=4×9=36,所以PT=6. 设圆O的半径为R,又CP=3,所以OP=R+3,OT=R,根据勾股定理,有OT2+PT2=OP2,可求出R=4.5.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案第22届冬奥会于2014年2月7日在俄罗斯的索契市举行. 中国队取得比较好的成绩,美中不足的是没有进入金牌榜前十名.不过,中国队在历届夏季奥运会上表现突出,从1984年美国洛杉矶奥运会至2012年英国伦敦奥运会,共获得金牌数量为201枚,具体每届获得的金牌数如下表所示:
| 届 数 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 金牌数 | 15 | 5 | 16 | 16 | 28 | 32 | 38 |
(1)请在上表填写2008年第29届北京奥运会中国所获得的金牌数;
(2)请求出上表中八届奥运会中国所获得的金牌数的平均数(保留整数);
(3)请将两幅统计图中不完整的部分补充完整;
 |
下列运算正确的是( )
|
| A. | (a﹣b)2=a2﹣b2 | B. |
| C. | 3a×ab=3a2b | D. | (x3)2=x5 |
 某中学九年级1班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.
某中学九年级1班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表. 请你根据图表中的信息回答下列问题:
请你根据图表中的信息回答下列问题:



