Question

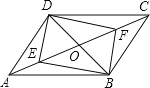
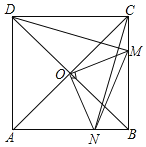
【题目】如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点（点M不与B、C重合），CN⊥DM，CN与AB交于点N，连接OM、ON、MN.下列四个结论：①△CNB≌△DMC；②△CON≌△DOM；③AN2＋CM2＝MN2；④若AB＝2，则S△OMN的最小值是.其中正确结论的个数是（ ）

A.1B.2C.3D.4

Answer 1

【答案】D

【解析】

①由正方形的性质得出CD=BC，∠BCD=90°，证出∠BCN=∠CDM，由ASA即可得出结论；

②由①得CM=BN，根据∠OCM=∠OBN=45°，OC=OB证明△OCM≌△OBN得OM=ON，∠COM=∠BON，进而证明∠DOM=∠CON，再根据DO=CO可证△CON≌△DOM（SAS）；

③根据AB=BC，CM=BN得BM=AN，在Rt△BMN中，BM2+BN2=MN2，从而AN2+CM2=MN2；

④先证明四边形BMON的面积是定值1，根据△MNB的面积最大时，△MNO的面积最小，设BN=x=CM，则BM=2-x，得△MNB的面积=x（2-x）=-x2+x，求出△MNB的面积最大值，从而得出结论.

∵正方形ABCD中，CD=BC，∠BCD=90°，

∴∠BCN+∠DCN=90°，

又∵CN⊥DM，

∴∠CDM+∠DCN=90°，

∴∠BCN=∠CDM，

又∵∠CBN=∠DCM=90°，

∴△CNB≌△DMC（ASA），故①正确；

根据△CNB≌△DMC，可得CM=BN，

又∵∠OCM=∠OBN=45°，OC=OB，

∴△OCM≌△OBN（SAS），

∴OM=ON，∠COM=∠BON，

∴∠DOC+∠COM=∠COB+∠BON，即∠DOM=∠CON，

又∵DO=CO，

∴△CON≌△DOM（SAS），故②正确；

∵AB=BC，CM=BN，

∴BM=AN，

又∵Rt△BMN中，BM2+BN2=MN2，

∴AN2+CM2=MN2，故③正确；

∵△OCM≌△OBN，

∴四边形BMON的面积=△BOC的面积=1，即四边形BMON的面积是定值1，

∴当△MNB的面积最大时，△MNO的面积最小，

设BN=x=CM，则BM=2-x，

∴△MNB的面积=x（2-x）=-x2+x=，

∴当x=1时，△MNB的面积有最大值，

此时S△OMN的最小值是1-=，故④正确；

综上所述，正确结论的个数是4个，

故选D．