Question

（2012•南通）如图，⊙O的半径为17cm，弦AB∥CD，AB=30cm，CD=16cm，圆心O位于AB，CD的上方，求AB和CD的距离．

Answer 1

分析：过点O作弦AB的垂线，垂足为E，延长AE交CD于点F，连接OA，OC；由于AB∥CD，则OF⊥CD，EF即为AB、CD间的距离；由垂径定理，易求得AE、CF的长，在构建的直角三角形中，根据勾股定理即可求出OE、OF的长，也就求出了EF的长，即弦AB、CD间的距离．

解答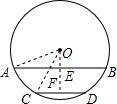：解：过点O作弦AB的垂线，垂足为E，延长OE交CD于点F，连接OA，OC，
∵AB∥CD，
∴OF⊥CD，
∵AB=30cm，CD=16cm，
∴AE=

1

2

AB=

1

2

×30=15cm，CF=

1

2

CD=

1

2

×16=8cm，
在Rt△AOE中，
OE=

OA2-AE2

=

172-152

=8cm，
在Rt△OCF中，
OF=

OC2-CF2

=

172-82

=15cm，
∴EF=OF-OE=15-8=7cm．
答：AB和CD的距离为7cm．

点评：本题考查的是勾股定理及垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．