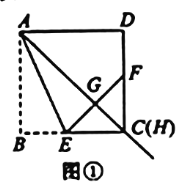
题目内容
【题目】在正方形![]() 中,过点A引射线
中,过点A引射线![]() ,交边
,交边![]() 于点H(H不与点D重合).通过翻折,使点B落在射线
于点H(H不与点D重合).通过翻折,使点B落在射线![]() 上的点G处,折痕
上的点G处,折痕![]() 交
交![]() 于E,连接E,G并延长
于E,连接E,G并延长![]() 交
交![]() 于F.
于F.
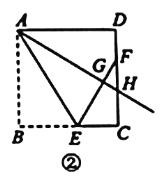
(1)如图1,当点H与点C重合时,![]() 与
与![]() 的大小关系是_________;
的大小关系是_________;![]() 是____________三角形.
是____________三角形.
(2)如图2,当点H为边![]() 上任意一点时(点H与点C不重合).连接
上任意一点时(点H与点C不重合).连接![]() ,猜想
,猜想![]() 与
与![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
(3)在图2,当![]() ,
,![]() 时,求
时,求![]() 的面积.
的面积.
【答案】(1)![]() ;等腰直角.(2)详见解析;(3)
;等腰直角.(2)详见解析;(3)![]()
【解析】
(1)连接AF,由正方形的性质及折叠的性质已知![]() ,由全等可知
,由全等可知![]() ,CF=CE,结合
,CF=CE,结合![]() 可确定
可确定![]() 是等腰直角三角形;(2)连接AF,由正方形的性质及折叠的性质已知
是等腰直角三角形;(2)连接AF,由正方形的性质及折叠的性质已知![]() ,即证
,即证![]() ;(3)设
;(3)设![]() ,依据题意及(2)的结论用含x的式子确定出
,依据题意及(2)的结论用含x的式子确定出![]() 的三边长,根据勾股定理求出x的值,即可求面积.
的三边长,根据勾股定理求出x的值,即可求面积.
解:(1)连接![]() ,
,
∵四边形![]() 是正方形,∴
是正方形,∴![]() ,
,![]() .
.
由翻折可知![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .…
.…
∴![]() .
.
又![]() 平分
平分![]()
∴AC垂直平分EF
∴![]()
∴![]() 是等腰直角三角形.
是等腰直角三角形.
故答案为:![]() ;等腰直角.
;等腰直角.
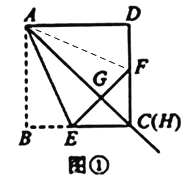
(2)连接![]() ,
,
∵四边形![]() 是正方形的对角线,∴
是正方形的对角线,∴![]() ,
,![]() .
.
由翻折可知![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .…
.…
∴![]() .…
.…
(3)设![]() ,则
,则![]() ,
,![]() .
.
在![]() 中,
中,![]() ,即
,即![]() .
.
解得![]() ,即
,即![]() 的长为
的长为![]() .
.
∴![]() ;…
;…
∴![]() .…
.…

练习册系列答案
相关题目
【题目】2019年6月11日至17日是我国第29个全国节能宣传周,主题为“节能减耗,保卫蓝天”。某学校为配合宣传活动,抽查了某班级10天的用电量,数据如下表(单位:度):
度数 | 8 | 9 | 10 | 13 | 14 | 15 |
天数 | 1 | 1 | 2 | 3 | 1 | 2 |
(1)这10天用电量的众数是___________,中位数是_________;
(2)求这个班级平均每天的用电量;
(3)已知该校共有20个班级,试估计该校6月份(30天)总的用电量.