Question

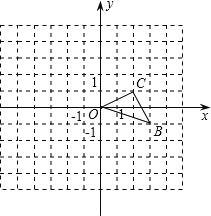
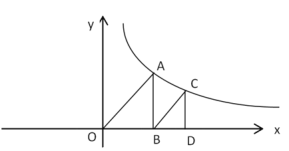
【题目】如下图，反比例函数（>0）图象上一点A，连结OA，作AB丄轴于点B，作BC∥OA交反比例函数图象于点C，作CD丄轴于点D,若点A、点C横坐标分别为m、n，则m：n的值为_______________．

Answer 1

【答案】

【解析】

根据题意得到A（m，），C（n，），则OB=m，OD=n，AB=，CD=，BD=n-m，证出△OAB∽△BCD，根据相似三角形对应边成比例即可求解．

解：∵点A、点C横坐标分别为m、n，
∴A（m，），C（n，），
∴OB=m，OD=n，AB=，CD=，
∴BD=n-m，

∵AB丄轴，CD丄轴，

∴∠ABO=∠CDO=90°，

∵BC∥OA，

∴∠AOB=∠CBD，

∴△OAB∽△BCD，

∴，即，

整理得，m2+mn-n2=0，

解得m=，（负数舍去），

∴m：n=．

故答案为：．