题目内容
7.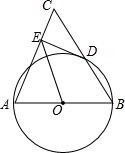 如图,已知在△ABC中,AB=AC,以AB为直径的⊙O交BC于D.
如图,已知在△ABC中,AB=AC,以AB为直径的⊙O交BC于D.(1)求证:BD=CD;
(2)过D作⊙O的切线交AC于E,若BC=4$\sqrt{3}$,AE=4,求sin∠AEO的值.
分析 (1)连接AD,根据圆周角定理得出AD⊥BC,然后根据等腰三角形三线合一的性质证得结论;
(2)连接OD,根据切线的性质得出OD⊥DE,根据中位线的性质得出OD∥AC,进一步得出DE⊥AC,∠AEO=∠EOD,根据射影定理求得CE,然后根据勾股定理求得ED,进而求得OE,解直角三角形求得sin∠EOD的值,从而求得sin∠AEO的值.
解答 解:(1)连接AD,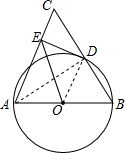
∵AB是直径,
∴AD⊥BC,
∵AB=AC,
∴BD=DC;
(2)连接OD,
∵DE是⊙O的切线,
∴OD⊥DE,
∵OA=0B,BD=CD,
∴OD∥AC,
∴DE⊥AC,∠AEO=∠EOD,
在RT△ADC中,DE⊥AC,
∴CD2=AC•CE,
∵CD=$\frac{1}{2}$BC=2$\sqrt{3}$,AE=4,
∴(2$\sqrt{3}$)2=(CE+4)•CE,解得CE=2,
∴AB=AC=4+2=6,
∴OD=3,
在RT△CDE中,ED=$\sqrt{C{D}^{2}-C{E}^{2}}$=$\sqrt{(2\sqrt{3})^{2}-{2}^{2}}$=2$\sqrt{2}$,
在RT△DOE中,OE=$\sqrt{E{D}^{2}+O{D}^{2}}$=$\sqrt{17}$,
∴sin∠EOD=$\frac{ED}{OE}$=$\frac{2\sqrt{2}}{\sqrt{17}}$=$\frac{2\sqrt{34}}{17}$,6
∴sin∠AEO=$\frac{2\sqrt{34}}{17}$.
点评 本题考查了切线的性质、圆周角定理、三角形中位线定理、勾股定理以及解直角三角形等,作出辅助线构建直角三角形是解题的关键.

练习册系列答案
相关题目
19.若二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M(x0,y0)在x轴下方,则代数式x02-(x1+x2)x0+x1x2的值( )
| A. | 等于0 | B. | 恒正 | C. | 恒负 | D. | 不能确定 |
17.在下列各选项中给出的三条线段不一定能组成三角形的是( )
| A. | a+1,a+2,a+3(a>0) | B. | 三条线段的比是4:6:8 | ||
| C. | 3cm,8cm,10cm | D. | 3a,5a,2a+1(a>0) |


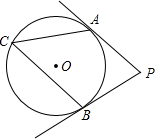 如图,PA、PB分别切⊙O于点A、B,若∠C=55°,则∠P的大小为70度.
如图,PA、PB分别切⊙O于点A、B,若∠C=55°,则∠P的大小为70度.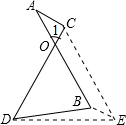 如图,线段AB=CD,AB与CD相交于点O,且∠1=60°,CE是由AB平移所得,试确定AC+BD与AB的大小关系,并说明原因.
如图,线段AB=CD,AB与CD相交于点O,且∠1=60°,CE是由AB平移所得,试确定AC+BD与AB的大小关系,并说明原因.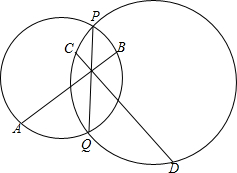 如图,PQ为两圆的公共弦,M为PQ上一点,AB、CD分别是两圆的弦且它们相交于M,求证:A、C、B、D四点共圆.
如图,PQ为两圆的公共弦,M为PQ上一点,AB、CD分别是两圆的弦且它们相交于M,求证:A、C、B、D四点共圆.