��Ŀ����
��ƽ��ֱ������ϵ�У����Ƕ���ֱ��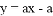 Ϊ������
������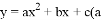 ��b��c������
��b��cΪ������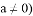 �ġ�����ֱ�ߡ�����һ���������������ϣ�����һ��������y���ϵ�������Ϊ�䡰���������Ρ���
�ġ�����ֱ�ߡ�����һ���������������ϣ�����һ��������y���ϵ�������Ϊ�䡰���������Ρ���
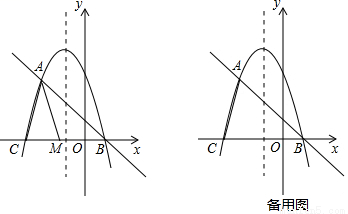
��֪������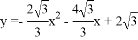 ���䡰����ֱ�ߡ�����A��B����
���䡰����ֱ�ߡ�����A��B���� ��A�ڵ�B�����
��A�ڵ�B����� ����x�Ḻ���ύ�ڵ�C��
����x�Ḻ���ύ�ڵ�C��
 ��գ��������ߵġ�����ֱ�ߡ��Ľ���ʽΪ______����A������Ϊ______����B������Ϊ______��
��գ��������ߵġ�����ֱ�ߡ��Ľ���ʽΪ______����A������Ϊ______����B������Ϊ______��
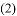 ��ͼ����MΪ�߶�CB��һ���㣬��
��ͼ����MΪ�߶�CB��һ���㣬��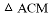 ��AM����ֱ��Ϊ�Գ��ᷭ�ۣ���C�ĶԳƵ�ΪN����
��AM����ֱ��Ϊ�Գ��ᷭ�ۣ���C�ĶԳƵ�ΪN����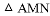 Ϊ�������ߵġ����������Ρ������N�����ꣻ
Ϊ�������ߵġ����������Ρ������N�����ꣻ
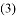 ����E�������ߵĶԳ������˶�ʱ���ڸ������ߵġ�����ֱ�ߡ��ϣ��Ƿ���ڵ�F��ʹ���Ե�A��C��E��FΪ������ı���Ϊƽ���ı��Σ������ڣ���ֱ��д����E��F�����ꣻ�������ڣ���˵�����ɣ�
����E�������ߵĶԳ������˶�ʱ���ڸ������ߵġ�����ֱ�ߡ��ϣ��Ƿ���ڵ�F��ʹ���Ե�A��C��E��FΪ������ı���Ϊƽ���ı��Σ������ڣ���ֱ��д����E��F�����ꣻ�������ڣ���˵�����ɣ�
 ��У����ϵ�д�
��У����ϵ�д�ijũ��300��ְ������51��������,�ƻ���ֲˮ��,�����߲�,��֪��ֲũ����ÿ����������Ͷ���������Ͷ����豸�ʽ����±���
ũ����Ʒ�� | ÿ�������Ͷ��� | ÿ������Ͷ���ʽ� |
ˮ�� | 4�� | 1��Ԫ |
�� | 8�� | 1��Ԫ |
�߲� | 5�� | 2��Ԫ |
��֪��ũ���ƻ����豸��Ͷ��67��Ԫ,Ӧ��������������ũ�������ֲ���,����ʹ���е�ְ�����й���,����Ͷ����ʽ����ù��ã�


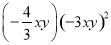 �Ľ��Ϊ__________��
�Ľ��Ϊ__________��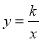 ��ͼ����һ�κ���y��mx��b��ͼ����A��1��3����B��n����1������.
��ͼ����һ�κ���y��mx��b��ͼ����A��1��3����B��n����1������.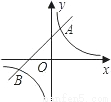

 BD
BD