题目内容
8.半径为5的圆O内有一点P,且OP=3,则过点P的最短弦长是8,最长弦长是10.分析 过点P的最长弦就是直径,最短弦就是垂直于OP的弦,根据垂径定理和勾股定理可求得.
解答 解:过点P的最长弦就是直径,5×2=10,
最短弦就是垂直于OP的弦,
如图所示,OP⊥CD于P,
∴OD=5,OP=3,
DP=$\sqrt{O{D}^{2}-O{P}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴弦CD=2DP=2×4=8.
故答案为:8、10.
点评 本题考查的是垂径定理,过圆内一点最长的弦是过这点的直径,最短的弦是过这点垂直于OP的弦,利用勾股定理可以求出最短的弦长.

练习册系列答案
相关题目
13.如表
从左到右每小格中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2014个格子与第2015个格子中的数之和为2.
| 3 | a | b | c | -1 | 2 | … |
18.下列四个多项式中,能因式分解的是( )
| A. | a2+4 | B. | a2-a+$\frac{1}{4}$ | C. | x2-5y | D. | x2+5y |
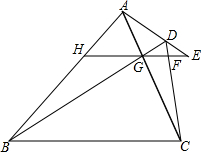 如图,已知△ABC、△DBC,AC与BD交于点G,过点G作EH∥BC分别交AB、DC、AD的延长线于点H、F、E,求证:EG2=EF•EH.
如图,已知△ABC、△DBC,AC与BD交于点G,过点G作EH∥BC分别交AB、DC、AD的延长线于点H、F、E,求证:EG2=EF•EH.