题目内容

已知：直线y=- $数学公式$ x+1与x轴、y轴分别交于A、B两点，以AB为边在第一象限内作正三角形ABC，⊙O′为△ABC的外接圆，与x轴交于另一点E．
（1）求C点坐标．
（2）求过点C与AB中点D的一次函数的解析式．
（3）求过E、O′、A三点的二次函数的解析式．

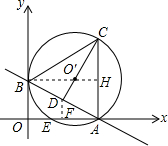解：（1）∵直线y=- $\text{[math]}$ x+1与x轴、y轴分别交于A、B两点，
∴A（ $\text{[math]}$ ，0），B（0，1），
在Rt△ABO中，
∵AB= $\text{[math]}$ =2，
∴tan∠BAO= $\text{[math]}$ = $\text{[math]}$ ，
∴∠BAO=30°
又∵△ABC是等边三角形
∴AC=AB=2，∠BAC=60°，
∴∠OAC=90°
∴CA∥OB，
∴C点坐标为（ $\text{[math]}$ ，2）；

（2）∵D是AB的中点，过D作DF∥OB，交OA于F，
则DF= $\text{[math]}$ OB= $\text{[math]}$ ，OF= $\text{[math]}$ OA= $\text{[math]}$
∴D点坐标为（ $\text{[math]}$ ， $\text{[math]}$ ），
设过C、D两点的一次函数解析式为y=kx+b（k≠0），
则 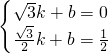$\text{[math]}$ ，解得 $\text{[math]}$ ，
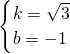∴所求一次函数的解析式为y= $\text{[math]}$ x-1；

（3）过点B作BH⊥AC于点H，
∵△ABC是等边△，
∴BH是AC的垂直平分线，
∴BF过点O′，
∵B（0，1），
∴当y=1时，x= $\text{[math]}$
∴O′（ $\text{[math]}$ ，1），
∵CA∥BO，BH⊥AC，
∴BH⊥OB，且过⊙O′半径的外端，
∴OB是⊙O′的切线，
∴OB²=OE•OA，即1=OE• $\text{[math]}$ ，解得OE= $\text{[math]}$ ，
∴E（ $\text{[math]}$ ，0），
设过E、O′、A三点的抛物线为y=ax2+bx+c，将三点坐标代入得
$\text{[math]}$

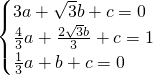
解得 $\text{[math]}$
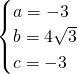
∴所求二次函数的解析式为y=-3x²+4 $\text{[math]}$ x-3．
分析：（1）先根据直线y=- $\text{[math]}$ x+1与x轴、y轴分别交于A、B两点求出A、B两点的坐标，在Rt△ABO中，根据勾股定理求出AB的长，故可得出tan∠BAO的值，可得出∠BAO的度数，判断出△ABC的形状，由平行线的判定定理得出CA∥OB，由此即可得出C点坐标；
（2）过D作DF∥OB，交OA于F，由点D是AB的中点可求出D点坐标，设过C、D两点的一次函数解析式为y=kx+b（k≠0），再把C、D两点的坐标代入即可求出此函数的解析式；
（3）过点B作BH⊥AC于点H，根据△ABC是等边△，可知BH是AC的垂直平分线，BH过点O′，故点B与点O′
的纵坐标相等，故可得出O′的坐标，再由CA∥BO，BH⊥AC可知BH⊥OB且过⊙O′半径的外端，故可得出OB是⊙O′的切线，由切线长定理可得OB²=OE•OA，进而可求出OE的长，故可得出E点坐标，
设过E、O′、A三点的抛物线为y=ax²+bx+c（a≠0），将三点坐标代入即可求出abc的值，故可得出结论．
点评：本题考查的是一次函数综合题，涉及到等边三角形的判定与性质、切线的判定与性质、用待定系数法求一次函数及二次函数的解析式等知识，难度适中．