题目内容
 已知:直线y=-2x+4交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线y=ax2+bx+c(a≠0)经过点A、B、C.
已知:直线y=-2x+4交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线y=ax2+bx+c(a≠0)经过点A、B、C.(1)求该抛物线的表达式;
(2)点D的坐标为(-3,0),点P为线段AB上的一点,当锐角∠PDO的正切值是
| 1 | 2 |
(3)在(2)的条件下,该抛物线上的一点E在x轴下方,当△ADE的面积等与四边形APCE的面积时,求点E的坐标.
分析:(1)根据直线解析式求出点A、B的坐标,再求出点C的坐标,然后利用待定系数法求二次函数解析式解答;
(2)根据点D的坐标求出OD的长,再根据∠PDO的正切值求出PD与y轴的交点F的坐标,然后利用待定系数法求出直线PD的解析式,再与直线y=-2x+4联立求解即可得到点P的坐标;
(3)设点E到x轴的距离为h,根据点A、C、D的坐标求出AC、AD的长,然后根据三角形的面积公式列式计算求出h,从而得到点E的纵坐标,再代入抛物线解析式求出点E的横坐标,即可得解.
(2)根据点D的坐标求出OD的长,再根据∠PDO的正切值求出PD与y轴的交点F的坐标,然后利用待定系数法求出直线PD的解析式,再与直线y=-2x+4联立求解即可得到点P的坐标;
(3)设点E到x轴的距离为h,根据点A、C、D的坐标求出AC、AD的长,然后根据三角形的面积公式列式计算求出h,从而得到点E的纵坐标,再代入抛物线解析式求出点E的横坐标,即可得解.
解答: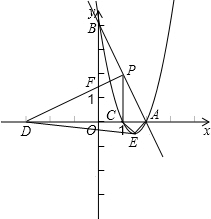 解:(1)令y=0,则-2x+4=0,
解:(1)令y=0,则-2x+4=0,
解得x=2,
令x=0,则y=4,
所以,点A(2,0),B(0,4),
∵AC=1,且OC<OA,
∴点C的坐标为(1,0),
∵抛物线y=ax2+bx+c(a≠0)经过点A、B、C,
∴
,
解得
,
∴该抛物线的表达式为y=2x2-6x+4;
(2)∵D的坐标为(-3,0),
∴OD=3,
设PD与y轴的交点为F,
∵∠PDO的正切值是
,
∴OF=
•OD=
×3=
,
∴点F的坐标为(0,
),
设直线PD的解析式为y=kx+b(k≠0,k、b为常数),
则
,
解得
,
所以,直线PD的解析式为y=
x+
,
联立
,
解得
,
∴点P的坐标为(1,2);
(3)设点E到x轴的距离为h,
∵A(2,0),(1,0),D(-3,0),
∴AC=1,AD=2-(-3)=5,
∵△ADE的面积等于四边形APCE的面积,
∴
×5h=
×1h+
×1×2,
解得h=
,
∵点E在x轴的下方,
∴点E的纵坐标为-
,
∴2x2-6x+4=-
,
整理得,4x2-12x+9=0,
解得x=
,
∴点E的坐标为(
,-
).
 解:(1)令y=0,则-2x+4=0,
解:(1)令y=0,则-2x+4=0,解得x=2,
令x=0,则y=4,
所以,点A(2,0),B(0,4),
∵AC=1,且OC<OA,
∴点C的坐标为(1,0),
∵抛物线y=ax2+bx+c(a≠0)经过点A、B、C,
∴
|
解得
|
∴该抛物线的表达式为y=2x2-6x+4;
(2)∵D的坐标为(-3,0),
∴OD=3,
设PD与y轴的交点为F,
∵∠PDO的正切值是
| 1 |
| 2 |
∴OF=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴点F的坐标为(0,
| 3 |
| 2 |
设直线PD的解析式为y=kx+b(k≠0,k、b为常数),
则
|
解得
|
所以,直线PD的解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
联立
|
解得
|
∴点P的坐标为(1,2);
(3)设点E到x轴的距离为h,
∵A(2,0),(1,0),D(-3,0),
∴AC=1,AD=2-(-3)=5,
∵△ADE的面积等于四边形APCE的面积,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得h=
| 1 |
| 2 |
∵点E在x轴的下方,
∴点E的纵坐标为-
| 1 |
| 2 |
∴2x2-6x+4=-
| 1 |
| 2 |
整理得,4x2-12x+9=0,
解得x=
| 3 |
| 2 |
∴点E的坐标为(
| 3 |
| 2 |
| 1 |
| 2 |
点评:本题是二次函数综合题型,主要考查了待定系数法求二次函数解析式,待定系数法求一次函数解析式,联立两直线解析式求交点坐标的方法,三角形的面积,综合题,但难度不大,作出图形更形象直观.

练习册系列答案
相关题目
 已知:直线y=-2x-2与x轴交于点A,与y轴交于点C,抛物线经过点A、C、E,且点E(6,7)
已知:直线y=-2x-2与x轴交于点A,与y轴交于点C,抛物线经过点A、C、E,且点E(6,7)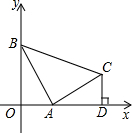 已知:直线y=-2x+2分别与x轴、y轴相交于点A、B,以线段AB为直角边在第一象限内作等腰直角△ABC,∠BAC=90°,过C作CD⊥x轴于D.求:
已知:直线y=-2x+2分别与x轴、y轴相交于点A、B,以线段AB为直角边在第一象限内作等腰直角△ABC,∠BAC=90°,过C作CD⊥x轴于D.求: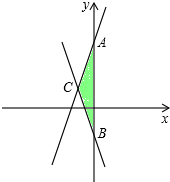 已知,直线y=2x+3与直线y=-2x-1.
已知,直线y=2x+3与直线y=-2x-1.