题目内容
计算下列各题:
(1)[3
÷(-
)×
]4-2(-3)3-(-5)2;
(2)4(x2-2xy)-3(xy-y2)+5(2x2-3y2);
(3)已知|2a+1|+4|b-4|+(c+1)2=0,求9a2b2-{ac2-[6a2b2+(4a2c-3ac2)]-6a2c}的值.
(1)[3
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 5 |
(2)4(x2-2xy)-3(xy-y2)+5(2x2-3y2);
(3)已知|2a+1|+4|b-4|+(c+1)2=0,求9a2b2-{ac2-[6a2b2+(4a2c-3ac2)]-6a2c}的值.
考点:整式的加减—化简求值,非负数的性质:绝对值,非负数的性质:偶次方,有理数的混合运算,整式的加减
专题:计算题
分析:(1)原式利用乘法分配律计算即可得到结果;
(2)原式去括号合并即可得到结果;
(3)原式去括号合并得到最简结果,利用非负数的性质求出a,b,c的值,代入原式计算即可得到结果.
(2)原式去括号合并即可得到结果;
(3)原式去括号合并得到最简结果,利用非负数的性质求出a,b,c的值,代入原式计算即可得到结果.
解答:解:(1)原式=(-
×
×
)4+54-25=1+54-25=30;
(2)原式=4x2-8xy-3xy+3y2+10x2-15y2=14x2-11xy-12y2;
(3)原式=9a2b2-ac2+6a2b2+4a2c-3ac2+6a2c=15a2b2+10a2c-4ac2,
∵|2a+1|+4|b-4|+(c+1)2=0,
∴a=-
,b=4,c=-1,
则原式=60-
+2=59.5.
| 10 |
| 3 |
| 3 |
| 2 |
| 1 |
| 5 |
(2)原式=4x2-8xy-3xy+3y2+10x2-15y2=14x2-11xy-12y2;
(3)原式=9a2b2-ac2+6a2b2+4a2c-3ac2+6a2c=15a2b2+10a2c-4ac2,
∵|2a+1|+4|b-4|+(c+1)2=0,
∴a=-
| 1 |
| 2 |
则原式=60-
| 5 |
| 2 |
点评:此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一元二次方程(2-k)x2+2x+1=0有两个不相等的实数根,则k的取值范围是( )
| A、k>1 |
| B、k>1且k≠2 |
| C、k>2 |
| D、k>-1且k≠2 |
无论x、y取何值,x2+y2-2x+12y+40的值都是( )
| A、正数 | B、负数 | C、零 | D、非负数 |
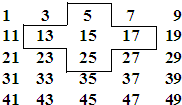 将连续的奇数1、3、5、7、9、…排成如图所示的数阵.
将连续的奇数1、3、5、7、9、…排成如图所示的数阵.