题目内容
问题:能比较两个数20102011和20112010的大小吗?为了解决这个问题,我们先把它抽象成数学问题,写出它的一般形式,即比较nn+1与(n+1)的大小(n是自然数),然后,我们从分析n=1,n=2,n=3,…这些简单情形入手,从中发现规律,经过归纳,猜想出结论.
(1)通过计算,比较下列各组中两个数的大小(在空格内填写“>”“=”或“<”
①12 21;②23 32;③34 43;④45 54;⑤56 65.
(2)从第(1)题的结果经过归纳,可猜想出nn+1与(n+1)n的大小关系是 .
(3)根据上面的归纳猜想得到的一般结论,试比较下面两个数的大小:20102011 20112010.
(1)通过计算,比较下列各组中两个数的大小(在空格内填写“>”“=”或“<”
①12
(2)从第(1)题的结果经过归纳,可猜想出nn+1与(n+1)n的大小关系是
(3)根据上面的归纳猜想得到的一般结论,试比较下面两个数的大小:20102011
考点:有理数大小比较,有理数的乘方
专题:阅读型
分析:根据有理数的乘方的定义分别进行计算,再进行比较即可;
(1)根据上述得出的答案分情况解答即可;
(2)根据(1)的结论解答即可.
(1)根据上述得出的答案分情况解答即可;
(2)根据(1)的结论解答即可.
解答:解:①12=1,21=2,则12<21;
②23=8,32=9,则23<32;
③34=81,43=64,则34>43;
④45=1024,54=625,则45>54;
⑤56>65;
故答案为:<,<,>,>,>;
(1)从上面的结果经过归纳,可以猜想出nn+1和(n+1)n的大小关系是:
当n<3时,nn+1<(n+1)n,
当n>3时,nn+1>(n+1)n;
故答案为:当n<3时,nn+1<(n+1)n,当n>3时,nn+1>(n+1)n;
(2)∵2010>3,
∴20102011>20112010.
故答案为:>.
②23=8,32=9,则23<32;
③34=81,43=64,则34>43;
④45=1024,54=625,则45>54;
⑤56>65;
故答案为:<,<,>,>,>;
(1)从上面的结果经过归纳,可以猜想出nn+1和(n+1)n的大小关系是:
当n<3时,nn+1<(n+1)n,
当n>3时,nn+1>(n+1)n;
故答案为:当n<3时,nn+1<(n+1)n,当n>3时,nn+1>(n+1)n;
(2)∵2010>3,
∴20102011>20112010.
故答案为:>.
点评:本题考查了有理数的乘方,有理数的大小比较,理解有理数的乘方的意义准确计算是解题的关键.

练习册系列答案
相关题目
从1~12这十二个自然数中任取一个,取到的数恰好是4的倍数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知点P关于x轴对称的点的坐标是(1,-2),则点P关于y轴对称的点的坐标是( )
| A、(1,2) |
| B、(-1,2) |
| C、(-1,-2) |
| D、(1,-2) |
 如图,△ABC中,∠ACB=90°,AC=3,BC=4.以A为圆心作圆与BC相切,则该圆的半径为( )
如图,△ABC中,∠ACB=90°,AC=3,BC=4.以A为圆心作圆与BC相切,则该圆的半径为( )| A、2.5 | B、3 | C、4 | D、5 |
 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3.
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3. 已知:如图,在△ABC中,∠ABC=30°,∠ACB=45°,AB=8,求BC的长.
已知:如图,在△ABC中,∠ABC=30°,∠ACB=45°,AB=8,求BC的长.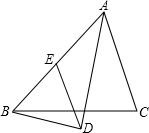 在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=5,求线段DE的长.
在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=5,求线段DE的长.