Question

【题目】如图，动点A，B从原点O同时出发，点A以每秒a个单位长度向x轴的负半轴向左运动，点B以每秒b个单位长度沿y轴的正半轴向上运动．

（1）若a，b满足关系|a+b﹣3|+（a﹣ b）2=0，请求出a，b的值；
（2）如图①，求当运动时间为2秒时，直线AB的函数表达式；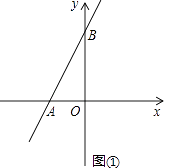

（3）如图②，∠BAO与∠ABO的外角平分线相交于点C，随着点A，点B的运动，∠C的度数是否会发生变化？若度数变化，请说明理由；若度数不变，请求出∠C的度数．

Answer 1

【答案】
（1）解：根据题意可得： ，

解得：

（2）解：由（1）知，当运动时间为2秒时，点A坐标为（﹣2，0），点B坐标为（0，4），

设直线AB解析式为y=mx+n，

将A（﹣2，0）、B（0，4）代入，得： ，

解得： ，

∴直线AB的解析式为y=2x+4

（3）解：随着点A，点B的运动，∠C的度数不会发生变化，

∵∠AOB=90°，

∴∠OAB+∠OBA=90°，

∴∠BAO与∠ABO的外角和为180°﹣∠OAB+180°﹣∠ABO=360°﹣（∠OAB+∠OBA）=270°，

∵AC、BC分别平分这两个外角，

∴∠CAB+∠CBA=135°，

∴∠C=45°

【解析】（1）根据非负数的性质可得关于a、b的方程组，求解可得；（2）由（1）中a、b的值可得点A、B的坐标，再用待定系数法即可求得解析式；（3）先求出△ABO两个外角度数为270°，再根据角平分线可得△ABC两个内角度数，从而可得∠C．
【考点精析】解答此题的关键在于理解解二元一次方程组的相关知识，掌握二元一次方程组：①代入消元法；②加减消元法，以及对确定一次函数的表达式的理解，了解确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法．