Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ō÷”–“ĽļŠĹō√ś «“ĽŇ◊őÔŌŖĶńňģ«Ģ£ģ“Ľīő£¨ňģ«ĢĻ‹ņŪ‘ĪĹę“Ľłý≥§![]() ĶńĪÍłň“Ľ∂ň∑Ň‘ŕňģ«ĢĶ◊≤ŅĶń
ĶńĪÍłň“Ľ∂ň∑Ň‘ŕňģ«ĢĶ◊≤ŅĶń![]() Ķ„£¨ŃŪ“Ľ∂ň¬∂≥Ųňģ√ś≤ĘŅŅ‘ŕňģ«ĢĪŖ‘ĶĶń
Ķ„£¨ŃŪ“Ľ∂ň¬∂≥Ųňģ√ś≤ĘŅŅ‘ŕňģ«ĢĪŖ‘ĶĶń![]() Ķ„£¨∑ĘŌ÷ĪÍłň”–
Ķ„£¨∑ĘŌ÷ĪÍłň”–![]() ĹĢ√Ľ‘ŕňģ÷–£¨¬∂≥Ųňģ√ś≤Ņ∑÷ĶńĪÍłň”Žňģ√ś≥…
ĹĢ√Ľ‘ŕňģ÷–£¨¬∂≥Ųňģ√ś≤Ņ∑÷ĶńĪÍłň”Žňģ√ś≥…![]() Ķńľ–Ĺ«£®ĪÍłň”ŽŇ◊őÔŌŖĶńļŠĹō√ś‘ŕÕ¨“Ľ∆Ĺ√śńŕ£©£ģ
Ķńľ–Ĺ«£®ĪÍłň”ŽŇ◊őÔŌŖĶńļŠĹō√ś‘ŕÕ¨“Ľ∆Ĺ√śńŕ£©£ģ

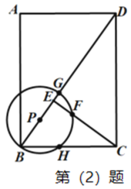
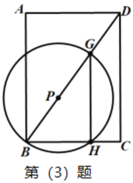
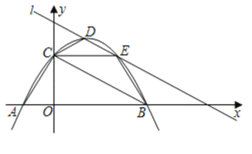
£®1£©“‘ňģ√śňý‘ŕ÷ĪŌŖő™![]() ÷Š£¨Ĺ®ŃĘ»ÁÕľňý ĺĶń÷ĪĹ«◊ÝĪÍŌĶ£¨«ůł√ňģ«ĢļŠĹō√śŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£®ĹŠĻŻĪ£ŃŰłýļŇ£©£Ľ
÷Š£¨Ĺ®ŃĘ»ÁÕľňý ĺĶń÷ĪĹ«◊ÝĪÍŌĶ£¨«ůł√ňģ«ĢļŠĹō√śŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£®ĹŠĻŻĪ£ŃŰłýļŇ£©£Ľ
£®2£©‘ŕ£®1£©ĶńŐűľĢŌ¬£¨«ůĶĪňģ√ś‘Ŕ…Ō…ż![]() ĪĶńňģ√śŅŪ‘ľő™∂ŗ…Ŕ£Ņ£®
ĪĶńňģ√śŅŪ‘ľő™∂ŗ…Ŕ£Ņ£®![]() »°
»°![]() £¨ĹŠĻŻĺę»∑ĶĹ
£¨ĹŠĻŻĺę»∑ĶĹ![]() £©£ģ
£©£ģ
°ĺīūįł°Ņ£®1£©![]() £Ľ£®2£©2.6m
£Ľ£®2£©2.6m
°ĺĹ‚őŲ°Ņ
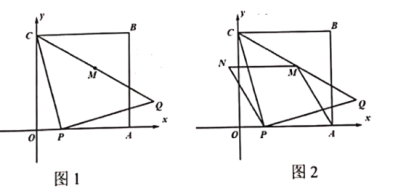
£®1£©łýĺ›ňýĹ®◊ÝĪÍŌĶ£¨…ŤĹ‚őŲ Ĺő™∂•Ķ„ Ĺ£ģ“Úīň–Ť«ů∂•Ķ„AĶń◊ÝĪÍļÕĶ„BĶń◊ÝĪÍ£ģ…ŤAB”Žx÷ŠĹĽ”ŕCĶ„£¨Ņ…÷™AC=1m£¨BC=0.5m£ģ◊ųBD°Õx÷Š”ŕĶ„D£ģÕ®ĻżĹ‚Rt°ųAOCļÕRt°ųBCD«ůĶ„A°ĘBĶń◊ÝĪÍ£ģ
£®2£©‘ň”√ļĮ ż–‘÷ ĹŠļŌĹ‚∑Ĺ≥Ő«ůĹ‚£ģ
Ĺ‚£ļ£®1£©…ŤAB”Žx÷ŠĹĽ”ŕCĶ„£¨Ņ…÷™AC=1m£¨BC=0.5m£ģ
◊ųBD°Õx÷Š”ŕĶ„D£ģ
‘ÚOA=0.5m£¨OC=![]() m£¨
m£¨
BD=![]() m£¨CD=
m£¨CD=![]() m£¨
m£¨
Ļ A£®0£¨-![]() £©£Ľ
£©£Ľ
B£®![]() £¨
£¨![]() £©£ģ
£©£ģ
…ŤŇ◊őÔŌŖĶńĹ‚őŲ Ĺő™y=ax2-![]() £ģ
£ģ
ĹęĶ„BĶń◊ÝĪÍīķ»ŽĶ√a=![]() £¨
£¨
“Ú∂Ýy=![]() £ģ
£ģ
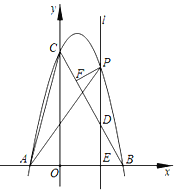
£®2£©ĶĪňģ√ś…Ō…ż![]() Ī£¨į—
Ī£¨į—![]() īķ»Ž
īķ»Ž![]()
«ůĶ√![]()
īň Īňģ√śŅŪ![]() m
m