��Ŀ����
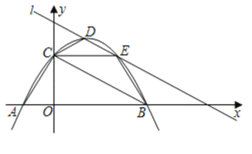
����Ŀ����ƽ��ֱ������ϵ�У���֪������y����![]() x2+bx+c��x�ύ��A(��1��0)��B(3��0)���㣬��y�ύ�ڵ�C��
x2+bx+c��x�ύ��A(��1��0)��B(3��0)���㣬��y�ύ�ڵ�C��
��1���������ߵĺ�������ʽ��
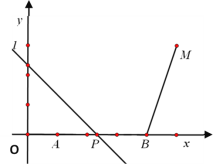
��2����ֱ��l����y����![]() x+m��������߽���D��E���㣬��ͼ��
x+m��������߽���D��E���㣬��ͼ��
������CD��CE��BE����S��BCE��3S��CDEʱ����m��ֵ��
���Ƿ����m��ֵ��ʹ��ԭ��O����ֱ��l�ĶԳƵ�P�պ����ڸ��������ϣ�������ڣ���ֱ��д��m��ֵ����������ڣ���˵�����ɣ�
���𰸡���1��y����![]() x2+
x2+![]() x+
x+![]() ����2����
����2����![]() ���ڴ��ڣ�
���ڴ��ڣ�![]()
��������
��1����A����1��0����B��3��0���������y����![]() x2+bx+cת��Ϊ�ⷽ���鼴�ɽ�����⣮
x2+bx+cת��Ϊ�ⷽ���鼴�ɽ�����⣮
��2��������֤��l��BC����S��BCE��3S��CDE���Ƴ�BC��3DE���Ƴ�ֱ��lӦ����BC���Ϸ�����BC��ȡһ��F��ʹ��BC��3BF���Ƴ��ı���BEDF��ƽ���ı��Σ���C��0��![]() ����B��3��0����BC��3BF���Ƴ�F��2��
����B��3��0����BC��3BF���Ƴ�F��2��![]() ������D��n��
������D��n��![]() n+m������E[n+1��
n+m������E[n+1��![]() ��n+1��+m]�������Ǵ��������ߵĽ���ʽ���ⷽ���鼴�ɽ�����⣮
��n+1��+m]�������Ǵ��������ߵĽ���ʽ���ⷽ���鼴�ɽ�����⣮
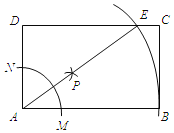
����ͼ2�У�����O��OM��BC����������M��M����������ֱ��l����OM��OM�����е㣬���������������M��M�������꼴�ɽ�����⣮
�⣺��1����A����1��0����B��3��0���������y����![]() x2+bx+c�ɵã�
x2+bx+c�ɵã�
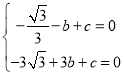 ��
��
��ã�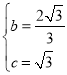 ��
��
�������ߵĽ���ʽΪy����![]() x2+
x2+![]() x+
x+![]() ��
��
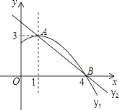
��2������ͼ��
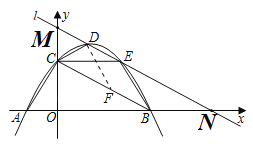
����y����![]() x2+
x2+![]() x+
x+![]() ����x��0���ɵ�y��
����x��0���ɵ�y��![]() ��
��
��C��0��![]() ����
����
��B��3��0����
��OC��![]() ��OB��3��
��OB��3��
��tan��CBO��![]() ��
��
���CBO��30����
��ֱ��l��y����![]() x+m��x�ύ��N��
x+m��x�ύ��N��![]() m��0����y�ύ��M��0��m����
m��0����y�ύ��M��0��m����
��tan��MNO��![]() ��
��![]() ��
��
���NMO��30������CBO��
��l��BC��
��S��BCE��3S��CDE��
��BC��3DE��
��ֱ��lӦ����BC���Ϸ���
��BC��ȡһ��F��ʹ��BC��3BF��
��BF��DE��
���ı���BEDF��ƽ���ı��Σ�
��C��0��![]() ����B��3��0����BC��3BF��
����B��3��0����BC��3BF��
��F��2��![]() ����
����
��D��n��![]() n+m������E[n+1����
n+m������E[n+1����![]() ��n+1��+m]�������Ǵ��������ߵĽ���ʽ�õ���
��n+1��+m]�������Ǵ��������ߵĽ���ʽ�õ���
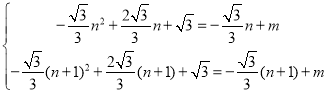 ��
��
��ã� ��
��
��m��ֵΪ![]() ��
��
����ͼ2�У�����O��OM��BC����������M��M����
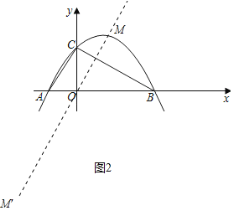
��ֱ��OM�Ľ���ʽΪy��![]() x��
x��
��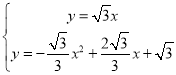 ��
��
��ã�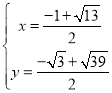 ��
�� ��
��
��M��![]() ��
��![]() ����M����
����M����![]() ��
��![]() ����
����
������ֱ��l����OM��OM�����е㣬
��![]() ��
��![]() ��
��
��ã�m��![]() ��
��

 Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д�
Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д� �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д�