题目内容
平面直角坐标系中,已知M(2,1)、N(2,6)两点,过反比例函数y=
的图象上任意一点P作y轴的垂线PG,G为垂足,O为坐标原点.若反比例函数y=
的图象与线段MN相交,则△OGP面积S的取值范围是( )
| k |
| x |
| k |
| x |
A、
| ||
| B、1≤S≤6 | ||
| C、2≤S≤12 | ||
| D、S≤2或S≥12 |
分析:根据反比例函数 y=
中k的几何意义,即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系,即S=
|k|.
| k |
| x |
| 1 |
| 2 |
解答: 解:根据题意可得:M(2,1),N(2,6)两点,反比例函数y=
解:根据题意可得:M(2,1),N(2,6)两点,反比例函数y=
与线段MN相交,
则k的范围是2≤k≤12;
则△OGP面积S为
k;
故△OGP面积S的取值范围是1≤S≤6.
故选B.
 解:根据题意可得:M(2,1),N(2,6)两点,反比例函数y=
解:根据题意可得:M(2,1),N(2,6)两点,反比例函数y=| k |
| x |
则k的范围是2≤k≤12;
则△OGP面积S为
| 1 |
| 2 |
故△OGP面积S的取值范围是1≤S≤6.
故选B.
点评:主要考查了反比例函数 y=
中k的几何意义,即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=
|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.
| k |
| x |
| 1 |
| 2 |

练习册系列答案
相关题目
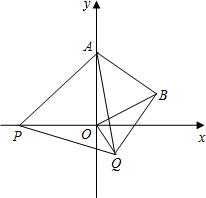 一边,在其一侧作等边三角形APQ.当点P运动到原点O处时,记Q的位置为B.
一边,在其一侧作等边三角形APQ.当点P运动到原点O处时,记Q的位置为B. 21、如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
21、如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.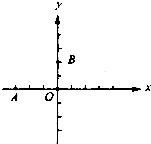 18、如图,在平面直角坐标系中,已知平行四边形的三个顶点坐标分别是O(0,0),A(-3,0),B(0,2),求平行四边形第四个顶点C的坐标.
18、如图,在平面直角坐标系中,已知平行四边形的三个顶点坐标分别是O(0,0),A(-3,0),B(0,2),求平行四边形第四个顶点C的坐标.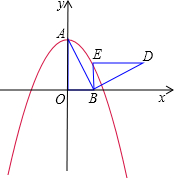 出M在抛物线内部(指抛物线与X轴所围成的部分)时t的取值范围.
出M在抛物线内部(指抛物线与X轴所围成的部分)时t的取值范围.