题目内容
（本题满分12分，第（1）题7分，第（2）题5分）
如图，在⊙O中，直径AB与弦CD垂直，垂足为E，连接AC，将△ACE沿AC翻折得到△ACF，直线FC与直线AB相交于点G．
（1）证明：直线FC与⊙O相切；
（2）若
，求证：四边形OCBD是菱形．
解：（1）连接
． ………………………………………1分
∵
， ∴
…………………………………………1分
由翻折得，
，
．…1分
∴
． …………………………………1分
∴OC∥AF．……………………………………1分
∴
．…………………………1分
∵点C在圆上
∴直线FC与⊙O相切． ………………………1分
（2）解一：在Rt△OCG中，∵
，∴
， …………1分
∵直径AB垂直弦CD， ∴
………………………1分
∴
………………………1分
∵
∴
． ………………………1分
∴四边形OCBD是菱形． ………………………1分
解二：在Rt△OCG中，∵，∴， ………………1分
∵
，∴
………………………1分
∵AB垂直于弦CD， ∴
………………………1分
∵直径AB垂直弦CD， ∴
………………………1分
∴四边形OCBD是平行四边形
∵AB垂直于弦CD，∴四边形OCBD是菱形． …………………………………1分
解析:略
练习册系列答案
教材全解字词句篇系列答案
相关题目
的
与x轴交于
、
两点，且点C在x轴的上方．
、B、C，求这二次函数的解析式；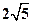
的
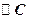与x轴交于
、
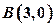两点，且点C在x轴的上方．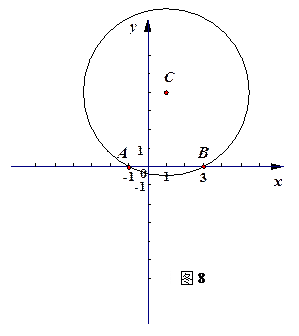
、B、C，求这二次函数的解析式；
M、A、B为顶点的四边形是平行四边形，请你直接写出点M的坐标.
=
，求证：
．
足为E，连接AC，将△ACE沿AC翻折得到△ACF，直线FC与直线AB相交于点G．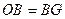
，求证：四边形OCBD是菱形．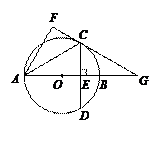
轴相交于点F，点Q为直线AD上一点，且△ABQ与△ADF相似，直接写出点Q点的坐标．