题目内容
 如图①,图②,图③,图④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第n个“广”字中的棋子个数是________.
如图①,图②,图③,图④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第n个“广”字中的棋子个数是________.
2n+5
分析:首先观察每个广字横有几个原点,然后观察撇有几个原点,找到规律后即可解答.
解答:由题目得,第1个“广”字中的棋子个数是7;
第2个“广”字中的棋子个数是9;
第3个“广”字中的棋子个数是11;
4个“广”字中的棋子个数是13;
发现第5个“广”字中的棋子个数是15…
进一步发现规律:第n个“广”字中的棋子个数是(2n+5).
故答案为:2n+5.
点评:本题是一图形的变化类问题,关键是通过归纳与总结,得到其中的规律.部分考生总结规律为第n个“广”字中的棋子个数是(2n+3)得到了错误答案.
分析:首先观察每个广字横有几个原点,然后观察撇有几个原点,找到规律后即可解答.
解答:由题目得,第1个“广”字中的棋子个数是7;
第2个“广”字中的棋子个数是9;
第3个“广”字中的棋子个数是11;
4个“广”字中的棋子个数是13;
发现第5个“广”字中的棋子个数是15…
进一步发现规律:第n个“广”字中的棋子个数是(2n+5).
故答案为:2n+5.
点评:本题是一图形的变化类问题,关键是通过归纳与总结,得到其中的规律.部分考生总结规律为第n个“广”字中的棋子个数是(2n+3)得到了错误答案.

练习册系列答案
相关题目
正方形ABCD与正方形CEFG的位置如图所示,点G在线段CD或CD的延长线上,分别连接BD、BF、FD,得到 BFD.
BFD.
(1)在图1、图2、图3中,若正方形CEFG的边长分别为1、3、4,且正方形ABCD的边长均为3,请通过计算填写下表:
图1 图2 图3
| 正方形CEFG的边长 | 1 | 3 | 4 |
 BFD的面积 BFD的面积 | | | |
 ,正方形ABCD的边长为
,正方形ABCD的边长为 ,猜想
,猜想 的大小,并结合图3证明你的猜想.
的大小,并结合图3证明你的猜想.  运动的路程s与运动时间t(秒)之间的函数图象,图3是点P的纵坐标y与点P运动的路程s之间的函数图象的一部分.
运动的路程s与运动时间t(秒)之间的函数图象,图3是点P的纵坐标y与点P运动的路程s之间的函数图象的一部分.
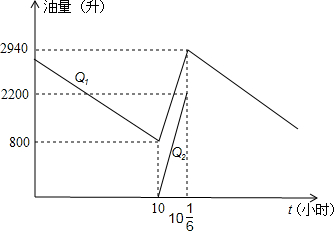 (1)求运输飞机起飞时油箱的油量;
(1)求运输飞机起飞时油箱的油量; 类似地,图2所示的算筹图我们可以表述为( )
类似地,图2所示的算筹图我们可以表述为( )
 B.
B. C.
C. D.
D.