��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У�������ABCD�Ķ���ֱ�ΪA��0��4����B����4��0����C��0����4����D��4��0��������ͼ��M���������¶��壺��PΪͼ��M������һ�㣬��QΪ������ABCD��������һ�㣬���P��Q�����ľ��������ֵ����ô��������ֵΪͼ��M�ġ������ࡱ������d��M����
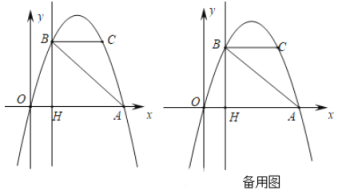
��1����֪��E��0��2����G����1����1����
����ͼ1��ֱ��д��d����E����d����G����ֵ��
����ͼ2������EOFԲ�Ľǡ�EOF=45�㣬������EOF�Ƶ�O˳ʱ����ת���ǣ�0������180�㣩�õ�����E'OF'����d������E'OF'��ȡ���ֵʱ������ǵ�ȡֵ��Χ��
��2����PΪƽ����һ���㣬������d����P��=6��ֱ��д��OP���ȵ�ȡֵ��Χ��

���𰸡���1����d(��E)=6��d(��G)![]() ����45�㣼����90���135�㣼����180�㣻��2��2��OP��
����45�㣼����90���135�㣼����180�㣻��2��2��OP��![]() ��
��
��������
(1)�ٸ��ݡ������ࡱ�Ķ��壬d(��E)=EC��d(��G)=GA��
�ڹ۲�ͼ���֪������OE��F����x����������y��ĸ������н���ʱ��d(����E��OF��)ȡ���ֵ���ɴ�д�����ķ�Χ���ɣ�
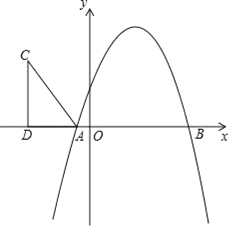
(2)��ͼ3�У��ֱ���A��B��C��DΪԲ�ģ�6Ϊ�뾶�������õ�ͼ�е�4����(����)������P��ͼ�к�����ʱ��d(��P)=6�����OP�����ֵ�Լ���Сֵ���ɽ�����⣮
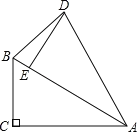
(1)����ͼ1�У�����AG��

�����⣺d(��E)=EC=6��d(��G)=GA![]() ��
��
�ڹ۲�ͼ���֪������OE'F'��x����������y��ĸ������н���ʱ��d(����E'OF')ȡ���ֵ��
����45�㣼����90���135�㣼����180��ʱ������������
(2)��ͼ3�У��ֱ���A��B��C��DΪԲ�ģ�6Ϊ�뾶�������õ�ͼ�е�4����(����)������P��ͼ�к�����ʱ��d(��P)=6��

��ͼ��P(m��m)��
��PB=6��
��m2+(4+m)2=36��
��ã�m=��2![]() ��2
��2![]() (����)��
(����)��
��P(��2![]() ����2
����2![]() )��
)��
��OP�����ֵ=OP![]() m=��2
m=��2![]() 2
2![]() ��
��
��OP����Сֵ=OP'=2��
��2��OP�ܩ�2![]() 2
2![]() ��
��