题目内容
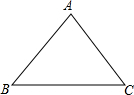 (1)如图△ABC,请用圆规和直尺作出的△ABC的外接圆.(不要求写作法,但要保留作图痕迹)
(1)如图△ABC,请用圆规和直尺作出的△ABC的外接圆.(不要求写作法,但要保留作图痕迹)(2)若△ABC是正三角形,边长为6,△ABC的外接圆的半径是多少?
分析:(1)分别作出AC和BC的垂直平分线,两线的交点就是圆心O的位置,再以CO长为半径画圆即可;
(2)当△ABC是正三角形时,BC的垂直平分线过A点,首先根据等腰三角形三线合一的性质计算出∠OCF=30°,再根据勾股定理计算出CO的长度即可.
(2)当△ABC是正三角形时,BC的垂直平分线过A点,首先根据等腰三角形三线合一的性质计算出∠OCF=30°,再根据勾股定理计算出CO的长度即可.
解答: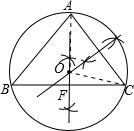 解:(1)如图所示:⊙O即为所求;
解:(1)如图所示:⊙O即为所求;
(2)当△ABC是正三角形时,BC的垂直平分线过A点,
连接AO,CO,
∵△ABC是正三角形,AF⊥BC,
∴∠FAC=
∠BAC=30°,CF=
BC=3,
∵AO=CO,
∴∠ACO=30°,
∴∠OCF=60°-30°=30°,
∴OF=
OC,
设OC=x,则OF=2x,
x2+32=(2x)2,
解得:x=±
,
∵x表示CO的长,
∴x=CO=
.
 解:(1)如图所示:⊙O即为所求;
解:(1)如图所示:⊙O即为所求;(2)当△ABC是正三角形时,BC的垂直平分线过A点,
连接AO,CO,
∵△ABC是正三角形,AF⊥BC,
∴∠FAC=
| 1 |
| 2 |
| 1 |
| 2 |
∵AO=CO,
∴∠ACO=30°,
∴∠OCF=60°-30°=30°,
∴OF=
| 1 |
| 2 |
设OC=x,则OF=2x,
x2+32=(2x)2,
解得:x=±
| 3 |
∵x表示CO的长,
∴x=CO=
| 3 |
点评:此题主要考查了三角形外接圆以及利用勾股定理,基本作图,关键是掌握如何确定三角形外接圆的圆心:其中两条边的垂直平分线的交点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知:如图△ABC中,AB=AC,CD、BE是△ABC的角平分线;
已知:如图△ABC中,AB=AC,CD、BE是△ABC的角平分线;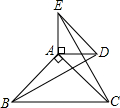 已知:如图△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°.
已知:如图△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°.

 (2012•宁津县一模)如图△ABC中BD和CE是两条高,∠A=45°,∠ADE=∠ABC,则
(2012•宁津县一模)如图△ABC中BD和CE是两条高,∠A=45°,∠ADE=∠ABC,则 如图△ABC的面积为a.
如图△ABC的面积为a.