题目内容
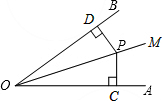如图，点P在射线OM上，PC⊥OA，PD⊥OB，垂足分别为C，D且PC=PD，求证：OC﹦OD．
证明：∵PC⊥OA，PD⊥OB，
∴∠PCO=∠PDO=90°，
在Rt△POC和Rt△POD中，
，
∴Rt△POC≌Rt△POD（HL），
∴OC=OD．
分析：利用“HL”证明Rt△POC和Rt△POD全等，根据全等三角形对应边相等证明即可．
点评：本题考查了全等三角形的判定与性质，熟练掌握直角三角形的判定方法并利用好公共边PO是解题的关键．
∴∠PCO=∠PDO=90°，
在Rt△POC和Rt△POD中，
，∴Rt△POC≌Rt△POD（HL），
∴OC=OD．
分析：利用“HL”证明Rt△POC和Rt△POD全等，根据全等三角形对应边相等证明即可．
点评：本题考查了全等三角形的判定与性质，熟练掌握直角三角形的判定方法并利用好公共边PO是解题的关键．
练习册系列答案
相关题目
（2012•五通桥区模拟）如图，已知∠MON=30°，AB⊥ON，垂足为点A，点B在射线OM上，AB=1cm，在射线ON上截取OA1=OB，过A1作A1B1∥AB，A1B1交射线OM于点B1，再在射线ON上截取OA2=OB1，过点A2作A2B2∥AB，A2B2交射线OM于点B2；…依次进行下去，则A1B1线段的长度为
如图，点P在射线OM上，PC⊥OA，PD⊥OB，垂足分别为C，D且PC=PD，求证：OC﹦OD．