题目内容
 如图,已知∠AOB,以O为端点作射线OC,且OE平分∠AOC,OF平分∠BOC.
如图,已知∠AOB,以O为端点作射线OC,且OE平分∠AOC,OF平分∠BOC.(1)如图①,若OC在∠AOB的内部,且∠EOF=65°,则∠AOB=
(2)如图①,若OC在∠AOB的内部,则一般地,∠AOB与∠EOF的数量关系是∠AOB=
(3)如图②,若OC在∠AOB的外部,则题(2)中的数量关系是否仍成立?并请说明理由.
考点:角的计算,角平分线的定义
专题:
分析:(1)根据角平分线的性质,可得出∠AOB=2∠EOF;
(2)根据角平分线的性质,可得出∠AOB=2∠EOF;
(3)设∠FOC=∠BOF=a,∠AOE=∠COE=b,分别表示出∠AOB及∠EOF,即可作出判断.
(2)根据角平分线的性质,可得出∠AOB=2∠EOF;
(3)设∠FOC=∠BOF=a,∠AOE=∠COE=b,分别表示出∠AOB及∠EOF,即可作出判断.
解答:解:(1)∠AOB=2∠EOF=130°;
(2)∠AOB=2∠EOF;
(3)数量关系依然成立.
设∠FOC=∠BOF=a,∠AOE=∠COE=b,
则∠EOF=∠FOC-∠COE=a-b,∠AOB=∠BOC-∠AOC=2(a-b),
故可得∠AOB=2∠EOF.
(2)∠AOB=2∠EOF;
(3)数量关系依然成立.
设∠FOC=∠BOF=a,∠AOE=∠COE=b,
则∠EOF=∠FOC-∠COE=a-b,∠AOB=∠BOC-∠AOC=2(a-b),
故可得∠AOB=2∠EOF.
点评:本题考查了角的计算,属于基础题,解答本题的关键是熟练掌握角平分线的性质.

练习册系列答案
相关题目
哈市4月份某天的最高气温是5℃,最低气温是-3℃,那么这天的温差最高气温减最低气温是( )℃.
| A、-2 | B、8 | C、-8 | D、2 |
如图是由四个相同立方体组成的立体图形的主视图和左视图,则原立体图形可能是( )


| A、①②③ | B、①②④ |
| C、①③④ | D、②③④ |
如果(a-1)-2=1成立,则( )
| A、a≠1 | B、a=0 |
| C、a=2 | D、a=0或a=2 |
 车厘子就是英语单词cherries(樱桃)的音译,车厘子的含铁量特别高,位于各种水果之首,常食车厘子可补充体内对铁元素的需求,促进血红蛋白再生,既可防治缺铁性贫血.又可增强体质,健脑益智,车厘子营养丰富,具有调中益气,健脾和胃,祛风湿,“令人面孔好颜色”之功效,对食欲不振,消化不良,风湿身痛等等均有益处.2011年1月份至6月份重庆市某商场车厘子销售价格y(元)与月份x(1≤x≤6且x为整数)之间的函数关系式如下表:
车厘子就是英语单词cherries(樱桃)的音译,车厘子的含铁量特别高,位于各种水果之首,常食车厘子可补充体内对铁元素的需求,促进血红蛋白再生,既可防治缺铁性贫血.又可增强体质,健脑益智,车厘子营养丰富,具有调中益气,健脾和胃,祛风湿,“令人面孔好颜色”之功效,对食欲不振,消化不良,风湿身痛等等均有益处.2011年1月份至6月份重庆市某商场车厘子销售价格y(元)与月份x(1≤x≤6且x为整数)之间的函数关系式如下表: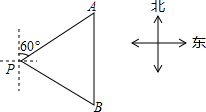 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行80海里后,到达B处,求此时轮船所在的B处相对于灯塔P的位置.(结果保留根号)
如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行80海里后,到达B处,求此时轮船所在的B处相对于灯塔P的位置.(结果保留根号)