题目内容
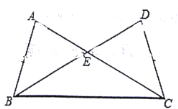
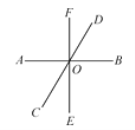
【题目】如图，直线AB、CD、EF相交于点O．
（1）写出∠COE的邻补角；
（2）分别写出∠COE和∠BOE的对顶角；
（3）如果∠BOD=60°，
，求∠DOF和∠FOC的度数．
【答案】（1）∠COF和∠EOD；（2）∠COE和∠BOE的对顶角分别为∠DOF和∠AOF；（3）∠DOF= 30°，∠FOC=150°
【解析】
（1）根据邻补角的定义可得结论；
（2）根据对顶角的定义可得结论；
（3）根据角的互余和互补，计算得解．
（1）∠COE的邻补角有∠COF和∠EOD；
（2）∠COE的对顶角为∠DOF，∠BOE的对顶角为∠AOF；
（3）∵
，
∴∠BOF=90°，
∴∠DOF= 90°-60°=30°，
∵∠DOF与∠FOC互为邻补角，
∴∠FOC=180°-30°=150°．
练习册系列答案
相关题目
【题目】某快递公司计划购买A型和B型两种货车共8辆，其中每辆车的价格以及每辆车的运载量如下表：
A型 | B型 | |
价格（万元/台） | m | n |
运载量（吨/车） | 20 | 30 |
若购买A型货车1辆，B型货车3辆，共需67万元；若购买A型货车3辆，B型货车2辆，共需75万元．
（1）求m，n的值；
（2）若每辆A型货车每月运载量500吨，每辆B型货车每月运载量750吨，为确保这8辆车每月的运载量总和不少于4750吨，且该公司购买A型和B型货车的总费用不超过124万元．请你设计一个方案，使得购车总费用最少．
