题目内容
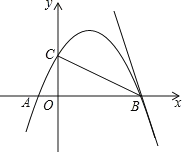
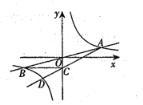
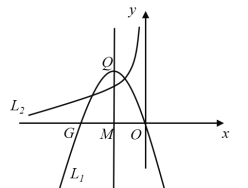
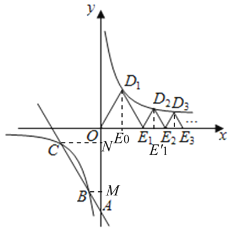
【题目】如图, 直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与双曲线
,与双曲线![]() 在第三象限交于
在第三象限交于![]() 两点,且
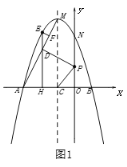
两点,且 ![]() ;下列等边三角形
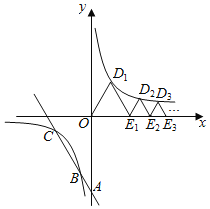
;下列等边三角形![]() ,
,![]() ,
,![]() ,……的边
,……的边![]() ,
,![]() ,
,![]() ,……在
,……在![]() 轴上,顶点
轴上,顶点![]() ……在该双曲线第一象限的分支上,则
……在该双曲线第一象限的分支上,则![]() = ____,前25个等边三角形的周长之和为 _______.
= ____,前25个等边三角形的周长之和为 _______.
【答案】![]() ; 60
; 60
【解析】
设![]() ,设直线与
,设直线与![]() 轴的交点为H,先求解
轴的交点为H,先求解![]() 的坐标,得到∠HAO=30°,用含
的坐标,得到∠HAO=30°,用含![]() 的代数式表示
的代数式表示![]() ,联立函数解析式利用根与系数的关系得到关于
,联立函数解析式利用根与系数的关系得到关于![]() 的方程,从而可得第一空的答案;过
的方程,从而可得第一空的答案;过![]() 分别向
分别向![]() 轴作垂线,垂足分别为
轴作垂线,垂足分别为![]()
![]() 先根据等边三角形的性质与反比例函数的性质求解
先根据等边三角形的性质与反比例函数的性质求解![]() 的边长,依次同法可得后面等边三角形的边长,发现规律,再前25个等边三角形的周长之和即可.
的边长,依次同法可得后面等边三角形的边长,发现规律,再前25个等边三角形的周长之和即可.
解:设![]() ,设直线与
,设直线与![]() 轴的交点为H,
轴的交点为H,
令![]() 则
则![]()
![]()
令![]() 则
则![]()
∴H(![]() ),又A(0,b),
),又A(0,b),
![]()
∴tan∠HAO=![]() ,∴∠HAO=30°,
,∴∠HAO=30°,
过![]() 作
作![]() 轴于
轴于![]()
![]() 作
作![]() 轴于
轴于![]() ,
,
∴AB=2BM,AC=2CN,∵BM=![]() ,
,![]() ,
,
∴AB=![]() ,AC=
,AC=![]() ,
,
∴![]() ,
,
联立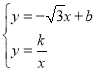
得到![]() 。
。
∴![]() ,由已知可得
,由已知可得![]() ,
,
∴![]() ,
,
∴反比例函数的解析式为![]() ,
,
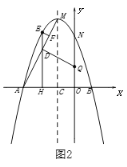
过![]() 分别向
分别向![]() 轴作垂线,垂足分别为
轴作垂线,垂足分别为![]()
![]()
设
由等边三角形的性质得:![]()
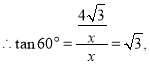
得:![]()
![]() (舍去)
(舍去)
经检验:![]() 符合题意,
符合题意,
![]()
可得![]() 的边长为4,
的边长为4,
同理设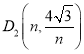 ,
,
![]()
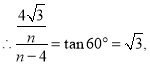
![]()
解得:![]() (舍去)
(舍去)
经检验:![]() 符合题意,
符合题意,
![]()
![]()
![]() 的边长为
的边长为![]() ,
,
同理可得:![]()
![]() 的边长为
的边长为![]() ,
,
![]()
![]() 的边长为
的边长为![]() .
.
∴前25个等边三角形的周长之和为![]()
=![]()
故答案为:![]()

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目