题目内容
△ABC内接于圆O,且AB=AC,圆O的半径等于6cm,O点到BC距离等于2cm,则AB长为________cm.
4 或4
或4
分析:按照圆心在三角形内部和外部两种情况,利用垂径定理,勾股定理分别计算.
解答: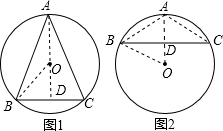 解:①当圆心在三角形内部时(如图1),
解:①当圆心在三角形内部时(如图1),
连接AO并延长交BC于D点,
∵AB=AC,
∴AD⊥BC,
依题意,得AO=BO=6,OD=2,
由勾股定理,得AB2-AD2=BO2-OD2=BD2,
AB2-(6+2)2=62-22,解得AB=4 ;
;
②当圆心在三角形外部时(如图2),
连接AO交BC于D点,
∵AB=AC,
∴AD⊥BC,
依题意,得AO=BO=6,OD=2,
由勾股定理,得AB2-AD2=BO2-OD2=BD2,
AB2-(6-2)2=62-22,解得AB=4 .
.
∴AB=4 或4
或4 cm.
cm.
故本题答案为:4 或4
或4 .
.
点评:本题考查了三角形的外接圆、等腰三角形的性质和勾股定理等知识的综合应用.还考查了分类讨论的思想.
 或4
或4
分析:按照圆心在三角形内部和外部两种情况,利用垂径定理,勾股定理分别计算.
解答:
 解:①当圆心在三角形内部时(如图1),
解:①当圆心在三角形内部时(如图1),连接AO并延长交BC于D点,
∵AB=AC,
∴AD⊥BC,
依题意,得AO=BO=6,OD=2,
由勾股定理,得AB2-AD2=BO2-OD2=BD2,
AB2-(6+2)2=62-22,解得AB=4
 ;
;②当圆心在三角形外部时(如图2),
连接AO交BC于D点,
∵AB=AC,
∴AD⊥BC,
依题意,得AO=BO=6,OD=2,
由勾股定理,得AB2-AD2=BO2-OD2=BD2,
AB2-(6-2)2=62-22,解得AB=4
 .
.∴AB=4
 或4
或4 cm.
cm.故本题答案为:4
 或4
或4 .
.点评:本题考查了三角形的外接圆、等腰三角形的性质和勾股定理等知识的综合应用.还考查了分类讨论的思想.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
 10、如图,正三角形ABC内接于圆O,动点P在圆周的劣弧AB上,且不与A,B重合,则∠BPC等于( )
10、如图,正三角形ABC内接于圆O,动点P在圆周的劣弧AB上,且不与A,B重合,则∠BPC等于( ) 40、如图,△ABC内接于圆O,∠A=50°,∠ABC=60°,BD是圆O的直径,BD交AC于点E,连接DC,则∠AEB等于( )
40、如图,△ABC内接于圆O,∠A=50°,∠ABC=60°,BD是圆O的直径,BD交AC于点E,连接DC,则∠AEB等于( ) 19、如图,正三角形ABC内接于圆O,P是BC所对劣弧上一点,求证:PA=PB+PC.
19、如图,正三角形ABC内接于圆O,P是BC所对劣弧上一点,求证:PA=PB+PC. 如图,△ABC为锐角三角形,△ABC内接于圆O,∠BAC=60°,H是△ABC的垂心,BD是⊙O的直径.
如图,△ABC为锐角三角形,△ABC内接于圆O,∠BAC=60°,H是△ABC的垂心,BD是⊙O的直径.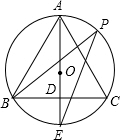 如图,正三角形ABC内接于圆O,AD⊥BC于点D交圆于点E,动点P在优弧BAC上,且不与点B,点C重合,则∠BPE等于
如图,正三角形ABC内接于圆O,AD⊥BC于点D交圆于点E,动点P在优弧BAC上,且不与点B,点C重合,则∠BPE等于