题目内容
如图，图中阴影部分表示x的取值范围，则下列表示中正确的是
- A.x＞-3＜2
- B.-3＜x≤2
- C.-3≤x≤2
- D.-3＜x＜2
B
分析：x表示-3右边的数，即大于-3，并且是2以及2左边的数，即小于或等于2的数．
解答：根据不等式组解集在数轴上的表示方法可知，不等式组的解集是指它们的公共部分．
A、不等式的表示方法是错的，应该是-3＜x＜2，
C、因为-3≤x≤2，在数轴上-3和2的点应该是实心的圆点；
D、因为-3＜x＜2，在数轴上-3和2的点应该是空心的圆点；
故选B．
点评：不等式组解集在数轴上的表示方法：把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．
分析：x表示-3右边的数，即大于-3，并且是2以及2左边的数，即小于或等于2的数．
解答：根据不等式组解集在数轴上的表示方法可知，不等式组的解集是指它们的公共部分．
A、不等式的表示方法是错的，应该是-3＜x＜2，
C、因为-3≤x≤2，在数轴上-3和2的点应该是实心的圆点；
D、因为-3＜x＜2，在数轴上-3和2的点应该是空心的圆点；
故选B．
点评：不等式组解集在数轴上的表示方法：把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．
练习册系列答案
相关题目
张师傅在铺地板时发现，用8块大小一样的长方形瓷砖恰好可以拼成一个大的长方形，如图1．然后，他用这8块瓷砖又拼出一个正方形，如图2，中间恰好空出一个边长为1的小正方形（阴影部分），假设长方形的长y，宽为x，且y＞x．
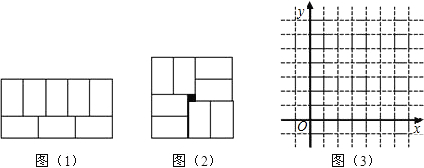
（1）请你求出图1中y与x的函数关系式；
（2）求出图2中y与x的函数关系式；
（3）在图3中作出两个函数的图象，写出交点坐标，并解释交点坐标的实际意义；
（4）根据以上讨论完成下表，观察x与y的关系，回答：如果给你任意8个相同的长方形，你能否拼成类似图1和图2的图形？说出你的理由．
（1）请你求出图1中y与x的函数关系式；
（2）求出图2中y与x的函数关系式；
（3）在图3中作出两个函数的图象，写出交点坐标，并解释交点坐标的实际意义；
（4）根据以上讨论完成下表，观察x与y的关系，回答：如果给你任意8个相同的长方形，你能否拼成类似图1和图2的图形？说出你的理由．
| 图（2）中小正方形边长 | 1 | 2 | 3 | 4 | … |
| x | 3 | 6 | 9 | 12 | … |
| y | 5 | 10 | 15 | 20 | … |
探索与应用
【列 式】
在边长为
的正方形中挖去一个边长为
的小正方形（＞）（如图甲），把余下的部分剪拼成一个长方形（如图乙），
试用、列式：
图甲中阴影部分的面积为 ，
图乙中阴影部分的面积为 。
【填 表】
根据表格所给的a、b的值，计算
与
的值，并将计算结果填入表中
| a | 2 | 0 | -2 | … |
| b | -3 | 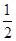 | 1 | … |
| | | | … |
| | | | … |
结合（1）、（2）中获得的经验，你能得出结论 ：
（填“>”，“=”或“<”）【应 用】
请你用你发现的结论进行简便运算：
（2010•新疆）张师傅在铺地板时发现，用8块大小一样的长方形瓷砖恰好可以拼成一个大的长方形，如图1．然后，他用这8块瓷砖又拼出一个正方形，如图2，中间恰好空出一个边长为1的小正方形（阴影部分），假设长方形的长y，宽为x，且y＞x．
（1）请你求出图1中y与x的函数关系式；
（2）求出图2中y与x的函数关系式；
（3）在图3中作出两个函数的图象，写出交点坐标，并解释交点坐标的实际意义；
（4）根据以上讨论完成下表，观察x与y的关系，回答：如果给你任意8个相同的长方形，你能否拼成类似图1和图2的图形？说出你的理由．
（1）请你求出图1中y与x的函数关系式；
（2）求出图2中y与x的函数关系式；
（3）在图3中作出两个函数的图象，写出交点坐标，并解释交点坐标的实际意义；
（4）根据以上讨论完成下表，观察x与y的关系，回答：如果给你任意8个相同的长方形，你能否拼成类似图1和图2的图形？说出你的理由．
| 图（2）中小正方形边长 | 1 | 2 | 3 | 4 | … |
| x | 3 | 6 | 9 | 12 | … |
| y | 5 | 10 | 15 | 20 | … |
（2010•新疆）张师傅在铺地板时发现，用8块大小一样的长方形瓷砖恰好可以拼成一个大的长方形，如图1．然后，他用这8块瓷砖又拼出一个正方形，如图2，中间恰好空出一个边长为1的小正方形（阴影部分），假设长方形的长y，宽为x，且y＞x．
（1）请你求出图1中y与x的函数关系式；
（2）求出图2中y与x的函数关系式；
（3）在图3中作出两个函数的图象，写出交点坐标，并解释交点坐标的实际意义；
（4）根据以上讨论完成下表，观察x与y的关系，回答：如果给你任意8个相同的长方形，你能否拼成类似图1和图2的图形？说出你的理由．
（1）请你求出图1中y与x的函数关系式；
（2）求出图2中y与x的函数关系式；
（3）在图3中作出两个函数的图象，写出交点坐标，并解释交点坐标的实际意义；
（4）根据以上讨论完成下表，观察x与y的关系，回答：如果给你任意8个相同的长方形，你能否拼成类似图1和图2的图形？说出你的理由．
| 图（2）中小正方形边长 | 1 | 2 | 3 | 4 | … |
| x | 3 | 6 | 9 | 12 | … |
| y | 5 | 10 | 15 | 20 | … |
探索与应用
【列 式】
在边长为
的正方形中挖去一个边长为
的小正方形（＞）（如图甲），把余下的部分剪拼成一个长方形（如图乙），
试用、列式：
图甲中阴影部分的面积为 ，
图乙中阴影部分的面积为 。
【填 表】
根据表格所给的a、b的值，计算
与
的值，并将计算结果填入表中
|
a |
2 |
0 |
-2 |
… |
|
b |
-3 |
|
1 |
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
【猜 想】
结合（1）、（2）中获得的经验，你能得出结论 ：
（填“>”，“=”或“<”）
【应 用】
请你用你发现的结论进行简便运算：