题目内容
探索与应用
【列 式】
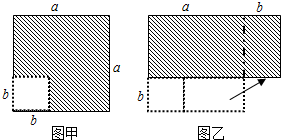
在边长为
的正方形中挖去一个边长为
的小正方形（＞）（如图甲），把余下的部分剪拼成一个长方形（如图乙），
试用、列式：
图甲中阴影部分的面积为 ，
图乙中阴影部分的面积为 。
【填 表】
根据表格所给的a、b的值，计算
与
的值，并将计算结果填入表中
| a | 2 | 0 | -2 | … |
| b | -3 | 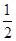 | 1 | … |
| | | | … |
| | | | … |
结合（1）、（2）中获得的经验，你能得出结论 ：
（填“>”，“=”或“<”）【应 用】
请你用你发现的结论进行简便运算：
【列 式】图甲中阴影部分的面积为，图乙中阴影部分的面积为
【填 表】
【猜 想】a 2 0 -2 … b -3 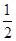1 … -5 
3 … -5 3 … = （填“>”，“=”或“<”）
【应 用】
.
解析试题分析：【列 式】根据长方形和正方形的面积公式结合图形的特征即可得到结果；
【填 表】分别把对应的数值代入得到的代数式计算即可得到结果；
【猜 想】仔细分析表中的计算数据即可判断；
【应 用】根据得到的结论结合所给式子的特征即可得到结果.
【列 式】试用、列式：图甲中阴影部分的面积为，
图乙中阴影部分的面积为；
【填 表】
根据表格所给的a、b的值，计算与的值，并将计算结果填入表中
【猜 想】a 2 0 -2 … b -3 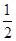1 … -5 3 … -5 3 …
结合（1）、（2）中获得的经验，你能得出结论 ： = （填“>”，“=”或“<”）
【应 用】
请你用你发现的结论进行简便运算：
.
考点：平方差公式的几何背景
点评：解答本题的关键是读懂题意，熟练运用长方形和正方形的面积公式结合图形的特征解题.
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
探索与应用探索与应用
【列 式】
在边长为
的正方形中挖去一个边长为
的小正方形（＞）（如图甲），把余下的部分剪拼成一个长方形（如图乙），
试用、列式：
图甲中阴影部分的面积为 ，
图乙中阴影部分的面积为 。
【填 表】
根据表格所给的a、b的值，计算
与
的值，并将计算结果填入表中
|
a |
2 |
0 |
-2 |
… |
|
b |
-3 |
|
1 |
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
【猜 想】
结合（1）、（2）中获得的经验，你能得出结论 ：
（填“>”，“=”或“<”）
【应 用】
请你用你发现的结论进行简便运算：
探索与应用
【列式】在边长为a的正方形中挖去一个边长为b的小正方形（a＞b）（如图甲），把余下的部分剪拼成一个长方形（如图乙），试用a、b列式：
图甲中阴影部分的面积为______，图乙中阴影部分的面积为______．
【填表】根据表格所给的a、b的值，计算a2-b2与（a+b）（a-b）的值，并将计算结果填入表中
| a | 2 | 0 | -2 | … |
| b | -3 |  | 1 | … |
| a2-b2 | ______ | ______ | ______ | … |
| （a+b）（a-b） | ______ | ______ | ______ | … |
【应用】请你用你发现的结论进行简便运算：43.7452-56.2552．