题目内容
抛物线y=-| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
分析:三个抛物线解析式都是顶点式,根据二次项系数判断开口方向;根据顶点式的坐标特点求顶点坐标及对称轴,判断是否相同.
解答:解:∵这三个函数的a值相同为-
,
故开口方向相同;
他们的顶点坐标分别为(0,1),(-1,0),(0,-
);
故对称轴,顶点坐标不同.
依次填:开口方向;对称轴,顶点坐标.
| 1 |
| 4 |
故开口方向相同;
他们的顶点坐标分别为(0,1),(-1,0),(0,-
| 1 |
| 4 |
故对称轴,顶点坐标不同.
依次填:开口方向;对称轴,顶点坐标.
点评:主要考查了二次函数的性质,以及对称轴和顶点坐标的判断.求抛物线的顶点坐标、对称轴及最值的方法.通常有两种方法:
(1)公式法:y=ax2+bx+c的顶点坐标为(-
,
),对称轴是x=-
;
(2)配方法:将解析式化为顶点式y=a(x-h)2+k,顶点坐标是(h,k),对称轴是x=h.
(1)公式法:y=ax2+bx+c的顶点坐标为(-
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
(2)配方法:将解析式化为顶点式y=a(x-h)2+k,顶点坐标是(h,k),对称轴是x=h.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

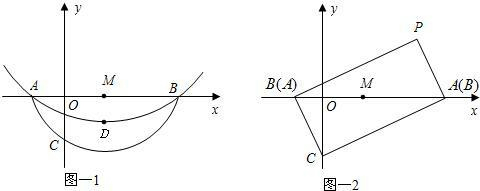
 (2012•相城区一模)如图,抛物线y=
(2012•相城区一模)如图,抛物线y= (2013•盐城模拟)如图,坐标系的原点为O,点P是第一象限内抛物线y=
(2013•盐城模拟)如图,坐标系的原点为O,点P是第一象限内抛物线y=