题目内容
8.平均数和中位数反映的都是数据的“集中程度”.设数据x1,…,x5的平均数为$\overline{x}$,中位数为m.(1)以数据2,3,5,8,12为例,分别计算A1,A2,B1,B2.
A1=|x1-m|+…+|x5-m|,A2=|x1-$\overline{x}$|+…+|x5-$\overline{x}$|,
B1=(x1-m)2+…+(x5-m)2,B2=(x1-$\overline{x}$)2+…+(x5-$\overline{x}$)2.
(2)根据计算结果,猜想平均数和中位数分别是什么意义下的数据代表值.
分析 (1)根据题意求得中位数,平均数,代入即可得到结论;
(2)根据平均数和中位数意义即可得到结论.
解答 解:(1)∵数据2,3,5,8,12的中位数是5,$\overline{x}$=$\frac{1}{5}$(2+3+5+8+12)=6,
∴m=5,$\overline{x}$=6,
∴A1=|x1-m|+…+|x5-m|=|2-5|+|3-5|+|5-5|+|8-5|+|12-5|=15,
A2=|x1-$\overline{x}$|+…+|x5-$\overline{x}$|=|2-6|+|3-6|+|5-6|+|8-6|+|12-6|=16,
B1=(x1-m)2+…+(x5-m)2=(2-5)2+(3-5)2+(5-5)2+(8-5)2+(12-5)2=71,
B2=(x1-$\overline{x}$)2+…+(x5-$\overline{x}$)2=(2-6)2+(3-6)2+(5-6)2+(8-6)2+(12-6)2=66.
(2)平均数:一组数据,用这组数据的总和除以总分数,得出的数就是这组数据的平均数.平均数的大小与一组数据里的每个数据都有关系,任何一个数据的变动都会引起平均数的变动,即平均数受较大数和较小数的影响.
中位数:将一组数据按大小依次排列,把处在最中间位置的一个数(或最中间位置的两个数的平均数)叫做这组数据的中位数.中位数的大小仅与数据的排列位置有关.因此中位数不受偏大和偏小数的影响,当一组数据中的个别数据变动较大时,常用它来描述这组数据的集中趋势.
点评 本题考查了中位数,绝对值,算术平均数的定义,熟记定义是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.下列各组线段中,能成比例的是( )
| A. | 3,6,7,9 | B. | 2,5,6,8 | C. | 3,6,9,18 | D. | 1,2,3,4 |

 如图1,直角三角形ABE,∠AEB=90°,∠BAE=30°,以AB为边作菱形ABCD,∠DAB=60°,点Q从A出发,沿折线AD-DC运动,运动到点C停止,设点Q运动的时间为t(s).△AEQ的面积s(cm2)与t(s)之间函数关系的图象由图2中的线段OP、PF给出.
如图1,直角三角形ABE,∠AEB=90°,∠BAE=30°,以AB为边作菱形ABCD,∠DAB=60°,点Q从A出发,沿折线AD-DC运动,运动到点C停止,设点Q运动的时间为t(s).△AEQ的面积s(cm2)与t(s)之间函数关系的图象由图2中的线段OP、PF给出.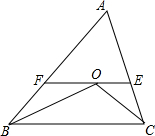 如图,△ABC中,BO,CO分别为∠ABC,∠ACB的平分线.交点为O,过O作EF平行于BC交AB,AC于F,E,探索BF+CE与FE的关系.说明理由.
如图,△ABC中,BO,CO分别为∠ABC,∠ACB的平分线.交点为O,过O作EF平行于BC交AB,AC于F,E,探索BF+CE与FE的关系.说明理由.