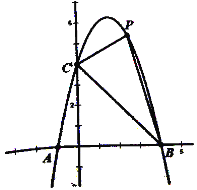
题目内容
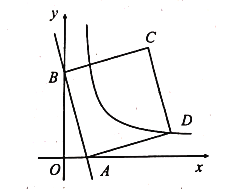
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,以
两点,以![]() 为边长在第一象限内作正方形
为边长在第一象限内作正方形![]() ,若反比例函数
,若反比例函数![]() (
(![]() )的图象经过顶点
)的图象经过顶点![]() .
.
(1)试确定![]() 的值;
的值;
(2)若正方形![]() 向左平移
向左平移![]() 个单位后,顶点
个单位后,顶点![]() 恰好落在反比例函数
恰好落在反比例函数![]() 的图象上,试确定
的图象上,试确定![]() 的值.
的值.
【答案】(1)![]() ;(2)4.
;(2)4.
【解析】
(1)作DG⊥x轴于点G,先求出A、B两点的坐标,故可得出OB=6,OA=2,再根据AAS定理得出△OAB≌![]() 可得出OG的长,进而得出D点坐标,把D点坐标代入反比例函数的解析式求出k的值即可;
可得出OG的长,进而得出D点坐标,把D点坐标代入反比例函数的解析式求出k的值即可;
(2)作CE⊥y轴,交反比例函数的图象于点G,同(1)可得![]() ≌
≌![]() ,OB=BC,OA=BE,故可得出C点坐标,把C点纵坐标代入(1)中的反比例函数解析式即可得出F点坐标,进而得出结论.
,OB=BC,OA=BE,故可得出C点坐标,把C点纵坐标代入(1)中的反比例函数解析式即可得出F点坐标,进而得出结论.
解:(1)对于函数![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,即
时,即![]() ,
,![]()
∴点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() .
.
过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,
,

则![]()
∵正方形![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]() ≌
≌![]()
∴![]() ,
,![]()
∴点![]() 坐标为
坐标为![]()
∵反比例函数![]() (
(![]() )的图象经过顶点
)的图象经过顶点![]() ,
,
∴![]() ,
,![]()
(2)过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,交双曲线于点
,交双曲线于点![]() .
.
由(1)易证![]() ≌
≌![]() .
.
∴![]() ,
,![]()
∴![]()
对于![]() ,当
,当![]() 时,
时,![]() ,
,![]()
∴点![]() 的坐标为
的坐标为![]() .
.
∴![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目