题目内容
若n2+n-1=0,求n3+2n2+2008的值.
考点:因式分解的应用
专题:
分析:将第二项拆开后前两项提取公因式即可整体代入求得答案.
解答:解:∵n2+n-1=0,
∴n2+n=1,
∴n3+2n2+2008=n3+n2+n2+2008=n(n2+n)+n2+2008=n2+n+2008=2009.
∴n2+n=1,
∴n3+2n2+2008=n3+n2+n2+2008=n(n2+n)+n2+2008=n2+n+2008=2009.
点评:此题考查了因式分解的应用,将所求式子进行适当的分解因式是解本题的关键.

练习册系列答案
相关题目
如果b-a=6,ab=7,则a2b-ab2的值是( )
| A、42 | B、-42 |
| C、13 | D、-13 |
在平面直角坐标系中,一个图案上各个点的横坐标和纵坐标分别加正数a,则所得的图案与原来图案相比( )
| A、形状不变,大小扩大到原来的a倍 |
| B、图案向右平移了a个单位 |
| C、图案向上平移了a个单位 |
| D、图案向右平移了a个单位,并且向上平移了a个单位 |
下列说法正确的是( )
| A、x的系数是0 |
| B、24与42不是同类项 |
| C、m的次数是0 |
| D、43abc是三次单项式 |

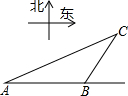 一艘轮船自西向东航行,在A处测得东偏北21.3°方向有一座小岛C,继续向东航行60海里到达B处,测得小岛C此时在轮船的东偏北63.5°方向上.
一艘轮船自西向东航行,在A处测得东偏北21.3°方向有一座小岛C,继续向东航行60海里到达B处,测得小岛C此时在轮船的东偏北63.5°方向上.