题目内容
6. 如图,D、E分别为△ABC的AB、AC边上两点,且AD=5,BD=3,AE=4,CE=6.求$\frac{DE}{BC}$的值.
如图,D、E分别为△ABC的AB、AC边上两点,且AD=5,BD=3,AE=4,CE=6.求$\frac{DE}{BC}$的值.
分析 由条件可得$\frac{AE}{AB}=\frac{AD}{AC}$,且∠A为公共角,则可证明△ADE∽△ACB,根据相似三角形的性质即可得到结论.
解答 解:∵AD=5,BD=3,AE=4,CE=6,
∴AB=8,AC=10,
∴$\frac{AE}{AB}$=$\frac{4}{8}$=$\frac{1}{2}$,$\frac{AD}{AC}=\frac{5}{10}=\frac{1}{2}$,
∴$\frac{AE}{AB}=\frac{AD}{AC}$,
∵∠A=∠A,
∴△ADE∽△ACB,
∴$\frac{DE}{BC}=\frac{AD}{AC}$=$\frac{1}{2}$.
点评 本题主要考查相似三角形的判定和性质,掌握三角形相似的判定方法,即有两组角对应相等、两组对应边的比相等且夹角相等或三组对应边的比相等是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.若a、b是非零实数,则下列说法正确的是( )
| A. | 若a2>a,则a>1 | B. | 若a2>a,则a2b>ab | ||
| C. | 若a2>a,则a2-b2>a-b2 | D. | 若a2>a,则-a2b<-ab |
15.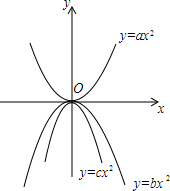 抛物线y=ax2、y=bx2、y=cx2的图象如图所示,则a、b、c的大小关系是( )
抛物线y=ax2、y=bx2、y=cx2的图象如图所示,则a、b、c的大小关系是( )
 抛物线y=ax2、y=bx2、y=cx2的图象如图所示,则a、b、c的大小关系是( )
抛物线y=ax2、y=bx2、y=cx2的图象如图所示,则a、b、c的大小关系是( )| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
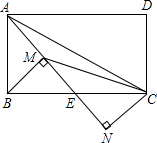 在矩形ABCD中,AD=$\sqrt{2}$AB,E为BC边的中点,过B、C两点分别作AE的垂线,M、N为垂足,连接CM、AC,则下列结论:
在矩形ABCD中,AD=$\sqrt{2}$AB,E为BC边的中点,过B、C两点分别作AE的垂线,M、N为垂足,连接CM、AC,则下列结论: