题目内容
7.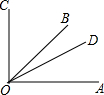 如图,已知∠COA=90°,∠COD比∠DOA大28°,且OB是∠COA的平分线.
如图,已知∠COA=90°,∠COD比∠DOA大28°,且OB是∠COA的平分线.①求∠BOD的度数;
②将已知条件中的28°改为32°,则∠BOD=16°;
③将已知条件中的28°改为n°,则∠BOD=($\frac{n}{2}$)°.
分析 (1)根据已知得出∠DOA+28°+∠DOA=90°,求出∠DOA,根据角平分线求出∠AOB,代入∠BOD=∠AOB-∠DOA求出即可;
(2)根据已知得出∠DOA+32°+∠DOA=90°,求出∠DOA,根据角平分线求出∠AOB,代入∠BOD=∠AOB-∠DOA求出即可;
(3)根据已知得出∠DOA+n°+∠DOA=90°,求出∠DOA,根据角平分线求出∠AOB,代入∠BOD=∠AOB-∠DOA求出即可.
解答 解:(1)∵∠COD比∠DOA大28°,
∴∠COD=∠DOA+28°,
∵∠AOC=90°,
∴∠COD+∠DOA=90°,
∴∠DOA+28°+∠DOA=90°,
∴∠DOA=31°,
∵OB是∠AOC的平分线,
∴∠AOB=∠BOC
=$\frac{1}{2}$∠AOC
=45°,
∴∠BOD=∠AOB-∠DOA
=45°-31°
=14°;
(2)∵∠COD比∠DOA大32°,
∴∠COD=∠DOA+32°,
∵∠AOC=90°,
∴∠COD+∠DOA=90°,
∴∠DOA+32°+∠DOA=90°,
∴∠DOA=29°,
∵OB是∠AOC的平分线,
∴∠AOB=∠BOC
=$\frac{1}{2}$∠AOC
=45°,
∴∠BOD=∠AOB-∠DOA
=45°-29°
=16°;
故答案为:16°;
(3)∵∠COD比∠DOA大n°,
∴∠COD=∠DOA+n°,
∵∠AOC=90°,
∴∠COD+∠DOA=90°,
∴∠DOA+n°+∠DOA=90°,
∴∠DOA=(45-$\frac{n}{2}$)°,
∵OB是∠AOC的平分线,
∴∠AOB=∠BOC
=$\frac{1}{2}$∠AOC
=45°,
∴∠BOD=∠AOB-∠DOA
=45°-(45-$\frac{n}{2}$)°
=($\frac{n}{2}$)°;
故答案为:($\frac{n}{2}$)°.
点评 本题考查了角平分线定义和角的有关计算的应用,能求出∠AOB和∠DOA的度数是解此题的关键.

| A. | 47,45 | B. | 45,45 | C. | 40,45 | D. | 47,45 |
| A. | 5 | B. | -1 | C. | 24 | D. | -30 |

| A. | ∠1=∠2 | B. | ∠1与∠2互余 | C. | ∠1=45° | D. | ∠2与∠AEF互补 |
| A. | b | B. | c | C. | $\frac{c+d}{2}$ | D. | $\frac{b+c}{2}$ |